题目内容
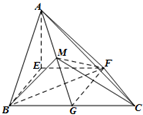 在直角梯形EFCB中,EF∥BC,EF=BE=
在直角梯形EFCB中,EF∥BC,EF=BE=| 1 |
| 2 |
(1)求证:AE∥平面BMF;
(2)求二面角G-MF-C的平面角的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)连接BF、GE,BF∩GE=0,连接OM,证明OM∥AE,由线面平行的判定定理可证AE∥平面BMF;
(2)利用面积射影法,求出S△MFC、S△OGC,即可求出二面角G-MF-C的平面角的余弦值.
(2)利用面积射影法,求出S△MFC、S△OGC,即可求出二面角G-MF-C的平面角的余弦值.
解答:
(1)证明:连接BF、GE,BF∩GE=0,连接OM,
∵EF∥BC,EF=BE=
BC=2,G是BC的中点,∠BEF=90°,
∴四边形EFGB为正方形,∠BFG=∠GFC=45°,
∴CF⊥BF,
∴O是EG的中点,
∵M是AG的中点,
∴OM∥AE,
∵AE?平面BMF,OM?平面BMF,
∴AE∥平面BMF;
(2)解:在△ABG中,cos∠AGB=
=
=
,
△MGC中,MG=
,CG=2,∴MC=
=
,
∴CF上的高为
=1,
∴S△MFC=
•2
•1=
,
∵OM∥AE,AE⊥面BCFE,
∴OM⊥面BCFE,
∴S△OGC=
•2•1=1,
∴二面角G-MF-C的平面角的余弦值为
=
=
.
∵EF∥BC,EF=BE=
| 1 |
| 2 |
∴四边形EFGB为正方形,∠BFG=∠GFC=45°,
∴CF⊥BF,
∴O是EG的中点,
∵M是AG的中点,
∴OM∥AE,
∵AE?平面BMF,OM?平面BMF,
∴AE∥平面BMF;
(2)解:在△ABG中,cos∠AGB=
| BG |
| AG |
| 2 | ||
2
|
| ||
| 3 |
△MGC中,MG=
| 3 |
3+4-2•
|
| 3 |
∴CF上的高为
| 3-2 |
∴S△MFC=
| 1 |
| 2 |
| 2 |
| 2 |
∵OM∥AE,AE⊥面BCFE,
∴OM⊥面BCFE,
∴S△OGC=
| 1 |
| 2 |
∴二面角G-MF-C的平面角的余弦值为
| S△OGC |
| S△MFC |
| 1 | ||
|
| ||
| 2 |
点评:本题考查了线面平行的证明,考查面面角的计算,考查了学生的推理论证能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
如图是一个体积为10的空间几何体的三视图,则图中x的值为( )


| A、2 | B、3 | C、4 | D、5 |
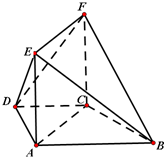 如图,在梯形ABCD中,AB∥CD,∠ABC=60°,AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.
如图,在梯形ABCD中,AB∥CD,∠ABC=60°,AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.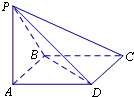 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且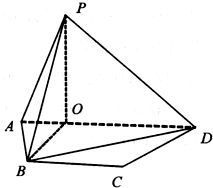 如图,等腰梯形ABCD中,AD∥BC,P是平面ABCD外一点,P在平面ABCD的射影O恰在AD上,PA=AB=BC=2AO=2,BO=
如图,等腰梯形ABCD中,AD∥BC,P是平面ABCD外一点,P在平面ABCD的射影O恰在AD上,PA=AB=BC=2AO=2,BO= 如图,PA,PB是圆O的两条切线,A,B是切点,C是劣弧AB(不包括端点)上一点,直线PC交圆O于另一点D,Q在弦CD上,且∠DAQ=∠PBC.求证:
如图,PA,PB是圆O的两条切线,A,B是切点,C是劣弧AB(不包括端点)上一点,直线PC交圆O于另一点D,Q在弦CD上,且∠DAQ=∠PBC.求证: