题目内容
已知不等式x2-2ax+2>0在x∈(-1,2)上恒成立,求实数a的取值范围.
考点:二次函数的性质,函数恒成立问题
专题:函数的性质及应用
分析:构造函数f(x),将不等式转化为求函数f(x)的最小值,利用二次函数对称轴与区间之间的关系即可求出结论.
解答:
解:设f(x)=x2-2ax+2,
判别式△=4a2-4×2=4a2-8,对称轴x=-
=a,
∵f(0)=2>0,
∴若判别式△<0,即-
<a<
.
若对称轴x=a>0,则满足条件
,
即
,
∴
≤a<
.
若对称轴x=a<0,则满足条件
,
即
,
∴
∴-
<a≤-
,
综上:-
<a<
,
即实数a的取值范围是:-
<a<
.
判别式△=4a2-4×2=4a2-8,对称轴x=-
| -2a |
| 2 |
∵f(0)=2>0,
∴若判别式△<0,即-
| 2 |
| 2 |
若对称轴x=a>0,则满足条件
|
即
|
∴
| 2 |
| 3 |
| 2 |
若对称轴x=a<0,则满足条件
|
即
|
∴
|
∴-
| 3 |
| 2 |
| 2 |
综上:-
| 3 |
| 2 |
| 3 |
| 2 |
即实数a的取值范围是:-
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题主要考查一元二次不等式恒成立问题,将不等式转化为函数是解决本题的关键.注意要分类讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
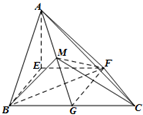 在直角梯形EFCB中,EF∥BC,EF=BE=
在直角梯形EFCB中,EF∥BC,EF=BE=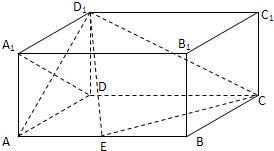 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.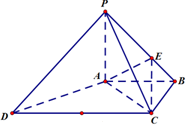 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC=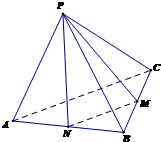 (文科)如图,正四面体P-ABC中,M为线段BC的中点,求异面直线PM与AC所成的角(结果用反三角函数值表示).
(文科)如图,正四面体P-ABC中,M为线段BC的中点,求异面直线PM与AC所成的角(结果用反三角函数值表示).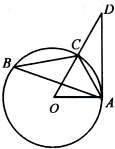 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠OAC=60°,AC=1,则AD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠OAC=60°,AC=1,则AD的长为