题目内容
(Ⅰ)一个骰子投掷2次,得到的点数分别为a,b,求直线y=a-b与函数y=sinx图象所有交点中相邻两个交点的距离都相等的概率.
(Ⅱ)若a是从区间[0,6]上任取一个数,b是从区间[0,6]上任取一个数,求直线y=a-b在函数y=sinx图象上方的概率.
(Ⅱ)若a是从区间[0,6]上任取一个数,b是从区间[0,6]上任取一个数,求直线y=a-b在函数y=sinx图象上方的概率.
考点:几何概型,古典概型及其概率计算公式
专题:计算题,概率与统计
分析:(Ⅰ)分别计算出一个骰子投掷2次,得到的点数分别为a,b的基本事件总数和满足直线y=a-b与函数y=sinx图象所有交点中相邻两个交点的距离都相等的基本事件个数,代入古典概型概率计算公式,可得答案;
(Ⅱ)确定试验全部结果构成的区域面积、直线y=a-b在函数y=sinx图象上方构成的区域面积,即可求出直线y=a-b在函数y=sinx图象上方的概率.
(Ⅱ)确定试验全部结果构成的区域面积、直线y=a-b在函数y=sinx图象上方构成的区域面积,即可求出直线y=a-b在函数y=sinx图象上方的概率.
解答:
 解:(Ⅰ)基本事件共36个:
解:(Ⅰ)基本事件共36个:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6). …(3分)
其中括号内第1个数表示a的取值,第2个数表示b的取值.
记“直线y=a-b与函数y=sinx图象所有交点中相邻两个交点的距离都相等”为事件A,则A={(a,b)|a-b=1或a-b=0或a-b=-1,1≤a≤6,1≤b≤6,a,b∈N}
∴事件A包含16个基本事件:
(2,1),(3,2),(4,3),(5,4),(6,5),(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),(1,2),(2,3),(3,4),(4,5),(5,6). …(5分)
∴所求事件的概率为P(A)=
=
. …(6分)
(Ⅱ)记“直线y=a-b在函数y=sinx图象上方”为事件B,试验全部结果构成的区域为Ω={(a,b)|0≤a≤6,0≤b≤6}…(7分)
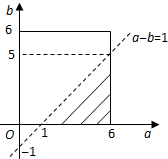
事件B的区域为{(a,b)|0≤a≤6,0≤b≤6,a-b>1},如图阴影部分所示:…(10分)
∴所求事件的概率为P(B)=
=
.…(12分)
 解:(Ⅰ)基本事件共36个:
解:(Ⅰ)基本事件共36个:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6). …(3分)
其中括号内第1个数表示a的取值,第2个数表示b的取值.
记“直线y=a-b与函数y=sinx图象所有交点中相邻两个交点的距离都相等”为事件A,则A={(a,b)|a-b=1或a-b=0或a-b=-1,1≤a≤6,1≤b≤6,a,b∈N}
∴事件A包含16个基本事件:
(2,1),(3,2),(4,3),(5,4),(6,5),(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),(1,2),(2,3),(3,4),(4,5),(5,6). …(5分)
∴所求事件的概率为P(A)=
| 16 |
| 36 |
| 4 |
| 9 |
(Ⅱ)记“直线y=a-b在函数y=sinx图象上方”为事件B,试验全部结果构成的区域为Ω={(a,b)|0≤a≤6,0≤b≤6}…(7分)
事件B的区域为{(a,b)|0≤a≤6,0≤b≤6,a-b>1},如图阴影部分所示:…(10分)
∴所求事件的概率为P(B)=
| ||
| 6×6 |
| 25 |
| 72 |
点评:本题考查的知识点是古典概型、几何概型的概率的计算公式,其中熟练掌握利用古典概型、几何概型的概率的计算求概率的步骤,是解答的关键.

练习册系列答案
相关题目
若曲线f(x)=alnx+bx3+csinx+d;(a,b,c,d均为常数)在x=2014处的切线方程为y+x-2014=0,则f(2014)+f′(2014)=( )
| A、2013 | B、2012 |
| C、-1 | D、0 |
已知ξ~N(0,62),且P(0≤ξ≤2)=0.2,则P(ξ<-2)等于( )
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |