题目内容
已知函数f(x)=lnx+
-1;
(1)求函数f(x)的单调区间及最值;
(2)证明:对任意的正整数n,1+
+
+…+
≥ln
都成立.
(3)是否存在过点(1,-1)的直线与函数y=f(x)的图象相切?若存在,有多少条?若不存在,说明理由.
| 1 |
| x |
(1)求函数f(x)的单调区间及最值;
(2)证明:对任意的正整数n,1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| en |
| n! |
(3)是否存在过点(1,-1)的直线与函数y=f(x)的图象相切?若存在,有多少条?若不存在,说明理由.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)f(x)的定义域为(0,+∞),f′(x)=
,由此能求出函数f(x)的单调区间及最值.
(Ⅱ)由(1)知f(x)=lnx-
≥f(1)=0,所以
≥1-lnx=ln
,取x=1,2,3,…,n,对得到的各式迭加能够证明对任意的正整数n,1+
+
+…+
≥ln
都成立.
(Ⅲ)假设存在这样的切线,设其中一个切点T(x0,lnx0-
),切线方程:y+1=
(x-1),由此利用导数性质推导出符合条件的切线有且仅有一条.
| x-1 |
| x2 |
(Ⅱ)由(1)知f(x)=lnx-
| x-1 |
| x |
| 1 |
| x |
| e |
| x |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| en |
| n! |
(Ⅲ)假设存在这样的切线,设其中一个切点T(x0,lnx0-
| x0-1 |
| x0 |
| x0-1 |
| x02 |
解答:
(Ⅰ)解:∵f(x)=lnx+
-1,
∴f(x)的定义域为(0,+∞),f′(x)=
.…(2分)
由f′(x)=0,得x=1.x∈(0,1)时,f′(x)0.
∴函数在(0,1)上是减函数,在(1,+∞)上是增函数,…(4分)
∴fmin(x)=f(1)=ln1=0,无最大值. …(5分)
(Ⅱ)证明:由(1)知f(x)=lnx-
≥f(1)=0,故
≥1-lnx=ln
,…(7分)
取x=1,2,3,…,n,得:
1≥lne,
≥ln
,
≥ln
,…,
≥ln
,
由上式迭加得:1+
+
+…+
≥ln
.
∴对任意的正整数n,1+
+
+…+
≥ln
都成立.…(9分)
(Ⅲ)解:假设存在这样的切线,设其中一个切点T(x0,lnx0-
),
切线方程:y+1=
(x-1),…(10分)
将点T坐标代入得:lnx0-
+1=
,即lnx0+
-
-1=0,①
设g(x)=lnx+
-
-1,则g′(x)=
. …(11分)
∵x>0,∴g(x)在区间(0,1),(2,+∞)上是增函数,在区间(1,2)上是减函数,
故g(x)极大值=g(1)=1>0,g(x)极小值=g(2)=ln2+
>0.…(12分)
又g(
)=ln
+12-16-1=-ln4-3<0,…(13分)
注意到g(x)在其定义域上的单调性,知g(x)=0仅在(
,1)内有且仅有一根
所以方程①有且仅有一解,故符合条件的切线有且仅有一条.…(14分)
| 1 |
| x |
∴f(x)的定义域为(0,+∞),f′(x)=
| x-1 |
| x2 |
由f′(x)=0,得x=1.x∈(0,1)时,f′(x)0.
∴函数在(0,1)上是减函数,在(1,+∞)上是增函数,…(4分)
∴fmin(x)=f(1)=ln1=0,无最大值. …(5分)
(Ⅱ)证明:由(1)知f(x)=lnx-
| x-1 |
| x |
| 1 |
| x |
| e |
| x |
取x=1,2,3,…,n,得:
1≥lne,
| 1 |
| 2 |
| e |
| 2 |
| 1 |
| 3 |
| e |
| 3 |
| 1 |
| n |
| e |
| n |
由上式迭加得:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| en |
| n! |
∴对任意的正整数n,1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| en |
| n! |
(Ⅲ)解:假设存在这样的切线,设其中一个切点T(x0,lnx0-
| x0-1 |
| x0 |
切线方程:y+1=
| x0-1 |
| x02 |
将点T坐标代入得:lnx0-
| x0-1 |
| x0 |
| (x0-1)2 |
| x02 |
| 3 |
| x0 |
| 1 |
| x02 |
设g(x)=lnx+
| 3 |
| x |
| 1 |
| x2 |
| (x-1)(x-2) |
| x3 |
∵x>0,∴g(x)在区间(0,1),(2,+∞)上是增函数,在区间(1,2)上是减函数,
故g(x)极大值=g(1)=1>0,g(x)极小值=g(2)=ln2+
| 1 |
| 4 |
又g(
| 1 |
| 4 |
| 1 |
| 4 |
注意到g(x)在其定义域上的单调性,知g(x)=0仅在(
| 1 |
| 4 |
所以方程①有且仅有一解,故符合条件的切线有且仅有一条.…(14分)
点评:本题考查函数单调区间和最值的求法,考查不等式的证明,考查满足条件的直线是否存在的判断与求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
在△ABC中,
•
=
•
,则△ABC是( )
| CB |
| CA |
| BC |
| BA |
| A、等腰直角三角形 |
| B、等边三角形 |
| C、等腰三角形 |
| D、直角三角形 |
已知函数f(x)=
,若存在实数t使得f(x)在R上为单调函数,则a的取值范围是( )
|
| A、a≥0 | B、a<0 |
| C、a≤t | D、a<-t |
执行如图所示的程序框图,输出的结果是15,则a的初始值m(m>0)有多少种可能( )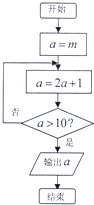

| A、1 | B、2 | C、3 | D、4 |