题目内容
已知抛物线C:y2=4x焦点为F,过F的直线交抛物线C于A,B两点,l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.
(1)求证:动点P在一条定直线上,并求此直线方程;
(2)设C、D为直线l1、l2与直线x=4的交点,△PCD面积为S1,△PAB面积为S2,求
的取值范围.
(1)求证:动点P在一条定直线上,并求此直线方程;
(2)设C、D为直线l1、l2与直线x=4的交点,△PCD面积为S1,△PAB面积为S2,求
| S1 |
| S2 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线中的最值与范围问题
分析:(1)设A(
,y1),B(
,y2)(y1>0>y2),设l1方程为y-y1=k1(x-
),由其余抛物线相切可得k1=
,l1方程为y=
x+
y1,同理l2方程为y=
x+
y2,联立l1、l2方程可得点P坐标为P(
,
),设直线AB的方程为x=ty+1,与抛物线方程联立及韦达定理可求得xP=-1,于是得到结论;
(2)由(1)知,C、D的坐标分别为C(4 ,
+
y1)、D(4 ,
+
y2).由三角形面积公式分别表示出S1,S2,根据
的形式可求其范围;
| y12 |
| 4 |
| y22 |
| 4 |
| y12 |
| 4 |
| 2 |
| y1 |
| 2 |
| y1 |
| 1 |
| 2 |
| 2 |
| y2 |
| 1 |
| 2 |
| y1y2 |
| 4 |
| y1+y2 |
| 2 |
(2)由(1)知,C、D的坐标分别为C(4 ,
| 8 |
| y1 |
| 1 |
| 2 |
| 8 |
| y2 |
| 1 |
| 2 |
| S1 |
| S2 |
解答:
解:(1)设A(
,y1),B(
,y2)(y1>0>y2),
易知l1斜率存在,设为k1,则l1方程为y-y1=k1(x-
),
由
,得k1y2-4y+4y1-k1y12=0,
由直线l1与抛物线C相切,知△=16-4k1(4y1-k1y12)=0,
于是,k1=
,l1方程为y=
x+
y1,
同理l2方程为y=
x+
y2,
联立l1、l2方程可得点P坐标为P(
,
),
设直线AB的方程为x=ty+1,与抛物线方程联立得y2-4ty-4=0.
y1+y2=4t,y1y2=-4,则xP=
=-1,
∴点P定在直线x=-1上.
(2)由(1)知,C、D的坐标分别为C(4 ,
+
y1)、D(4 ,
+
y2).
∴| CD |=| (
+
y1)-(
+
y2) |=|
|.
∴S1=S△PCD=
| 4-
|•|
|=
|y1-y2|,
S2=S△PAB=
•
|y1-y2|,
=
∈(0,
].
| y12 |
| 4 |
| y22 |
| 4 |
易知l1斜率存在,设为k1,则l1方程为y-y1=k1(x-
| y12 |
| 4 |
由
|
由直线l1与抛物线C相切,知△=16-4k1(4y1-k1y12)=0,
于是,k1=
| 2 |
| y1 |
| 2 |
| y1 |
| 1 |
| 2 |
同理l2方程为y=
| 2 |
| y2 |
| 1 |
| 2 |
联立l1、l2方程可得点P坐标为P(
| y1y2 |
| 4 |
| y1+y2 |
| 2 |
设直线AB的方程为x=ty+1,与抛物线方程联立得y2-4ty-4=0.
y1+y2=4t,y1y2=-4,则xP=
| y1y2 |
| 4 |
∴点P定在直线x=-1上.
(2)由(1)知,C、D的坐标分别为C(4 ,
| 8 |
| y1 |
| 1 |
| 2 |
| 8 |
| y2 |
| 1 |
| 2 |
∴| CD |=| (
| 8 |
| y1 |
| 1 |
| 2 |
| 8 |
| y2 |
| 1 |
| 2 |
| (y1y2-16)(y1-y2) |
| 2y1y2 |
∴S1=S△PCD=
| 1 |
| 2 |
| y1y2 |
| 4 |
| (y1y2-16)(y1-y2) |
| 2y1y2 |
| 25 |
| 4 |
S2=S△PAB=
| 1 |
| 2 |
| |-2-2t2| | ||
|
| 1+t2 |
| S1 |
| S2 |
| 25 |
| 4(1+t2) |
| 25 |
| 4 |
点评:该题考查抛物线的方程性质、直线与抛物线的位置关系、切线等知识,考查学生的运算求解及推理论证能力,综合性较强,难度较大.

练习册系列答案
相关题目
阅读如图的程序框图,运行相应的程序,若输出S=
,则判断框内应填入( )

| 2013 |
| 2014 |

| A、i≥2014 |
| B、i≥2015 |
| C、i>2014 |
| D、i>2015 |
执行如图所示的程序框图,输出的结果是15,则a的初始值m(m>0)有多少种可能( )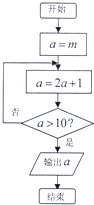

| A、1 | B、2 | C、3 | D、4 |


