题目内容
已知函数f(x)=(
)2(x>1).
(1)求函数的反函数;
(2)若不等式(1-
)f-1(x)>m(m-
)对[
,
]上的每一个x值都成立,求实数m的取值范围.
| x-1 |
| x+1 |
(1)求函数的反函数;
(2)若不等式(1-
| x |
| x |
| 1 |
| 4 |
| 1 |
| 2 |
考点:反函数,函数恒成立问题
专题:函数的性质及应用
分析:(1)由已知得
=
,整理,得x=
,x,y互换,得函数的反函数.
(2)由已知得1+
>m(m-
)成立,需f(
)>0且f(
)>0,解得-1<m<
.由此能求出实数m的取值范围.
| x-1 |
| x+1 |
| y |
1+
| ||
1-
|
(2)由已知得1+
| x |
| x |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
解答:
解:(1)∵f(x)=y=(
)2,x>1,
∴
=
,整理,得x=
,
x,y互换,得y=
,0<x<1,
∴函数的反函数f-1(x)=
(0<x<1)
(2)欲使不等式(1-
)f-1(x)>m(m-
)对[
,
]上的每一个x值都成立,
即1+
>m(m-
)成立,
令
=t,
≤t≤
,即1+t>m(m-t)在[
,
]成立,令f(t)=(1+m)t+1-m2,
则需f(
)>0且f(
)>0,解得-1<m<
.
∴实数m的取值范围是(-1,
).
| x-1 |
| x+1 |
∴
| x-1 |
| x+1 |
| y |
1+
| ||
1-
|
x,y互换,得y=
1+
| ||
1-
|
∴函数的反函数f-1(x)=
1+
| ||
1-
|
(2)欲使不等式(1-
| x |
| x |
| 1 |
| 4 |
| 1 |
| 2 |
即1+
| x |
| x |
令
| x |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
则需f(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
∴实数m的取值范围是(-1,
| 3 |
| 2 |
点评:本题考查反函数的求法,考查实数的取值范围的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
设函数f(x)=
,则满足f(x)=4的x的值是( )
|
| A、2 | B、16 |
| C、2或16 | D、-2或16 |
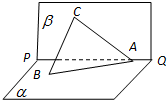 已知直二面角α-PQ-β,A∈PQ,B∈α,C∈β,CA=CB,∠BAP=45°,直线CA和平面α所成的角为30°.
已知直二面角α-PQ-β,A∈PQ,B∈α,C∈β,CA=CB,∠BAP=45°,直线CA和平面α所成的角为30°.