题目内容
(1)已知tanx=2,求
的值;
(2)已知
,
不共线,
=3
+5
,
=m
-3
.当m为何值时,
与
共线?
| cosx+sinx |
| cosx-sinx |
(2)已知
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
考点:三角函数的化简求值,平行向量与共线向量
专题:三角函数的求值
分析:(1)利用商的关系将式子弦化切,再把tanα的值代入化简即可;
(2)由向量共线的条件得:
=λ
,把条件代入列出方程求出m的值即可.
(2)由向量共线的条件得:
| c |
| d |
解答:
解:(1)由题意得,
=
=
=-3;(6分)
(2)当
与
共线时,有
=λ
,
则3
+5
=λ(m
-3
),即(3-λm)
+(5+3λ)
=
,
因为
,
不共线,所以
,
解得
,
故当m=-
时,
与
共线.
| cosx+sinx |
| cosx-sinx |
| 1+tanx |
| 1-tanx |
| 1+2 |
| 1-2 |
(2)当
| c |
| d |
| c |
| d |
则3
| a |
| b |
| a |
| b |
| a |
| b |
| 0 |
因为
| a |
| b |
|
解得
|
故当m=-
| 9 |
| 5 |
| c |
| d |
点评:本题考查考查齐次式:弦化切的应用,以及向量共线的条件,属于较基础题.

练习册系列答案
相关题目
 2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示.问:
2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示.问: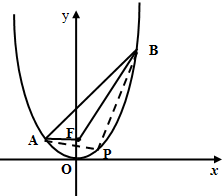 如图,已知抛物线x2=4y上两定点A,B分别在对称轴左、右两侧,F为抛物线的焦点,且|AF|=2,|BF|=5.
如图,已知抛物线x2=4y上两定点A,B分别在对称轴左、右两侧,F为抛物线的焦点,且|AF|=2,|BF|=5.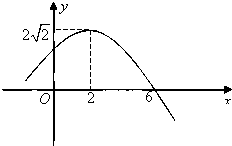 已知函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0,|φ|<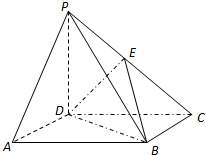 如图所示,PD⊥底面ABCD,四边形ABCD是正方形,PD=DC,E是PC的中点.
如图所示,PD⊥底面ABCD,四边形ABCD是正方形,PD=DC,E是PC的中点.