题目内容
(1)求y=
lg(tanx-1)的定义域;
(2)求y=
sin(
-3x)+1,x∈[0,
]的值域.
| sinx |
(2)求y=
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
考点:正切函数的单调性,函数的定义域及其求法,函数的值域
专题:函数的性质及应用,三角函数的图像与性质
分析:(1)由根式内部的代数式大于等于0,使函数y=lg(tanx-1)的真数大于0,建立不等关系,解不等式即可求出所求.
(2)由题意利用正弦函数的定义域和值域,求得f(x)的值域.
(2)由题意利用正弦函数的定义域和值域,求得f(x)的值域.
解答:
解:(1)由
,
解sinx≥0得:2kπ≤x≤2kπ+π,k∈Z;
解tanx-1>0得:
+kπ<x<kπ+
,k∈Z.
取交集得:
+2kπ<x<2kπ+
,k∈Z.
∴函数y=
lg(tanx-1)的定义域为{x|
+2kπ<x<2kπ+
,k∈Z}.
(2)若x∈[0,
],则
-3x∈[-
,
],
∴sin(
-3x)∈[-1,
],
∴
sin(
-3x)∈[-
,
],
故y=
sin(
-3x)+1的值域为[
,
].
|
解sinx≥0得:2kπ≤x≤2kπ+π,k∈Z;
解tanx-1>0得:
| π |
| 4 |
| π |
| 2 |
取交集得:
| π |
| 4 |
| π |
| 2 |
∴函数y=
| sinx |
| π |
| 4 |
| π |
| 2 |
(2)若x∈[0,
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
∴sin(
| π |
| 6 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 4 |
故y=
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| 5 |
| 4 |
点评:本题以对数函数的定义域的求解为载体,重点考查了三角不等式的求解,是基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
函数f(x)=x+
( )
| 2 |
| x |
| A、是奇函数,但不是偶函数 |
| B、既是奇函数,又是偶函数 |
| C、是偶函数,但不是奇函数 |
| D、既不是奇函数,又不是偶函数 |
若a=0.95.1,b=5.10.9,c=log0.95.1,则a、b、c三者的大小关系是( )
| A、a<b<c |
| B、b<c<a |
| C、c<b<a |
| D、c<a<b |
已知集合P={x|x≥0},Q={x|
≥0},则P∩Q=( )
| x+1 |
| x-2 |
| A、(-∞,2) |
| B、(-∞,-1) |
| C、[0,+∞) |
| D、(2,+∞) |
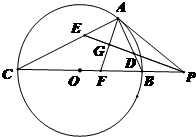 如图:已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB,AC于点D,E,.点G是线段ED的中点,AG的延长线与CP相交于点F.
如图:已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB,AC于点D,E,.点G是线段ED的中点,AG的延长线与CP相交于点F.