题目内容
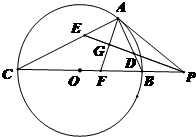 如图:已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB,AC于点D,E,.点G是线段ED的中点,AG的延长线与CP相交于点F.
如图:已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB,AC于点D,E,.点G是线段ED的中点,AG的延长线与CP相交于点F.(Ⅰ)证明:AF⊥ED;
(Ⅱ)当F恰为PC的中点时,求
| PB |
| PC |
考点:与圆有关的比例线段
专题:立体几何
分析:(Ⅰ)由弦切角定理得∠PAB=∠C,由角平分线性质得∠APE=∠CPE,从而∠ADE=∠AEP,由此能证明AF⊥ED.
(Ⅱ)由切割线定理得PA2=PB•PC,从而得到
PC2=PB•PC,由此能证明
=
.
(Ⅱ)由切割线定理得PA2=PB•PC,从而得到
| 1 |
| 4 |
| PB |
| PC |
| 1 |
| 4 |
解答:
选修4-1:几何证明选讲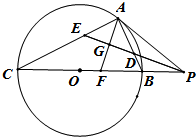
(Ⅰ)证明:如图,直线PA与圆O相切于点A,
∴由弦切角定理得∠PAB=∠C,
∵∠APC的平分线分别交AB,AC于点D,E,∴∠APE=∠CPE,
∵∠ADE=∠PAB+∠APE,∠AEP=∠C+∠CPE,
∴∠ADE=∠AEP,
∵G是DE的中点,∴AF⊥ED.
(Ⅱ)∵直线PA与圆O相切于点A,
∴PA2=PB•PC,
∵PA=PF=
PC,
∴
PC2=PB•PC,∴PC=4PB,
∴
=
.

(Ⅰ)证明:如图,直线PA与圆O相切于点A,
∴由弦切角定理得∠PAB=∠C,
∵∠APC的平分线分别交AB,AC于点D,E,∴∠APE=∠CPE,
∵∠ADE=∠PAB+∠APE,∠AEP=∠C+∠CPE,
∴∠ADE=∠AEP,
∵G是DE的中点,∴AF⊥ED.
(Ⅱ)∵直线PA与圆O相切于点A,
∴PA2=PB•PC,
∵PA=PF=
| 1 |
| 2 |
∴
| 1 |
| 4 |
∴
| PB |
| PC |
| 1 |
| 4 |
点评:本题考查两线段垂直的证明,考查两线段比值的求法,是中档题,解题时要认真审题,注意弦切角定理和切割线定理的合理运用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
若平面向量
=(3,5),
=(-2,1),则
-2
的坐标为( )
| a |
| b |
| a |
| b |
| A、(7,3) |
| B、(7,7) |
| C、(1,7) |
| D、(1,3) |
已知幂函数f(x)=(m-3)xm,则下列关于f(x)的说法不正确的是( )
| A、f(x)的图象过原点 |
| B、f(x)的图象关于原点对称 |
| C、f(x)的图象关于y轴对称 |
| D、f(x)=x4 |
复数
对应的点位于( )
| 1-i |
| 2-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
