题目内容
若sin(π-θ)=
,求
+
的值(提示,先化简,在将sinθ=
代入化简式即可)
| 1 |
| 3 |
| cos(π+θ) |
| [cos(π-θ)-1]•cosθ |
| cos(θ-2π) | ||||
sin(θ-
|
| 1 |
| 3 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:先化简已知条件以及所求表达式,再将sinθ=
代入化简式即可.
| 1 |
| 3 |
解答:
解:sin(π-θ)=
,
可得sinθ=
,
则
+
=
+
=
-
=0.
| 1 |
| 3 |
可得sinθ=
| 1 |
| 3 |
则
| cos(π+θ) |
| [cos(π-θ)-1]•cosθ |
| cos(θ-2π) | ||||
sin(θ-
|
=
| cosθ |
| (cosθ-1)•cosθ |
| cosθ |
| -cosθ•cosθ+cosθ |
=
| 1 |
| cosθ-1 |
| 1 |
| cosθ-1 |
=0.
点评:本题考查诱导公式的应用,三角函数的化简求值.考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若平面向量
=(3,5),
=(-2,1),则
-2
的坐标为( )
| a |
| b |
| a |
| b |
| A、(7,3) |
| B、(7,7) |
| C、(1,7) |
| D、(1,3) |
在下列给出的函数:(1)y=
;(2)y=
;(3)y=x2+x中,幂函数的个数为( )
| x |
| 1 |
| x2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
已知幂函数f(x)=(m-3)xm,则下列关于f(x)的说法不正确的是( )
| A、f(x)的图象过原点 |
| B、f(x)的图象关于原点对称 |
| C、f(x)的图象关于y轴对称 |
| D、f(x)=x4 |
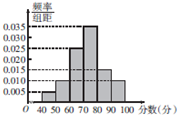 某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )
某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )| A、120 | B、150 |
| C、180 | D、200 |