题目内容
已知直线l的极坐标方程为ρcosθ-ρsinθ=a(a∈R),曲线C的参数方程为
(θ为参数),若曲线C关于直线l对称,则a= .
|
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:首先,讲给定的直线的极坐标方程化为直角坐标方程,曲线的参数方程化为普通方程,然后,根据直线关于圆的对称,得到该直线必过圆的圆心,建立等式,求解即可.
解答:
解:∵直线l的极坐标方程为ρcosθ-ρsinθ=a(a∈R),
∴它的直角坐标方程为:x-y-a=0,
曲线C的参数方程为
(θ为参数),
它的普通方程为:(x+1)2+y2=1,
∵曲线C关于直线l对称,
故该直线必过圆心(-1,0),
代入,直线的直角坐标方程,得到
-1-0-a=0,
∴a=-1,
故答案为:-1.
∴它的直角坐标方程为:x-y-a=0,
曲线C的参数方程为
|
它的普通方程为:(x+1)2+y2=1,
∵曲线C关于直线l对称,
故该直线必过圆心(-1,0),
代入,直线的直角坐标方程,得到
-1-0-a=0,
∴a=-1,
故答案为:-1.
点评:本题重点考查了直线的极坐标方程和直角坐标方程的互化,圆的参数方程和普通方程互化等知识,圆关于直线的对称问题等知识,属于中档题.

练习册系列答案
相关题目
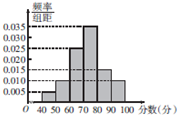 某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )
某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )| A、120 | B、150 |
| C、180 | D、200 |
方程x2+3x-3=0的解在区间( )
| A、(0,1)内 |
| B、(1,2)内 |
| C、(2,3)内 |
| D、以上均不对 |