题目内容
化简:sin2(
+α)+tan(
-α)tan(π-α).
| π |
| 2 |
| 3π |
| 2 |
考点:二倍角的余弦,运用诱导公式化简求值
专题:三角函数的求值
分析:利用诱导公式以及同角三角函数的基本关系式,化简求解即可.
解答:
解:sin2(
+α)+tan(
-α)tan(π-α)
=cos2α-cotαtanα
=cos2α-1
=
cos2α-
.
| π |
| 2 |
| 3π |
| 2 |
=cos2α-cotαtanα
=cos2α-1
=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查诱导公式的应用,三角函数的化简求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线l过点A(1,2),且不经过第四象限,则直线l的斜率的取值范围( )
A、[0,
| ||
| B、[0,1] | ||
| C、[0,2] | ||
D、(0,
|
复数
对应的点位于( )
| 1-i |
| 2-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设点(3,4)为奇函数y=f(x)图象上的点,则下列各点在函数图象上的是( )
| A、(-3,4) |
| B、(3,-4) |
| C、(-3,-4) |
| D、(-4,-3) |
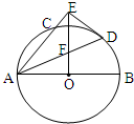 如图,AB是☉O的直径,AC是弦,∠BAC的平分线AD交☉O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是☉O的直径,AC是弦,∠BAC的平分线AD交☉O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.