题目内容
在平面直角坐标系xOy中,圆C的方程为x2+y2-4x=0.若直线y=k(x+1)上存在一点P,使过P所作的圆的两条切线相互垂直,则实数k的取值范围是( )
A、(-∞,-2
| ||||||||
B、[-2
| ||||||||
C、[-
| ||||||||
D、(-∞,-2
|
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:由题意可得圆心为C(2,0),半径R=2;设两个切点分别为A、B,则由题意可得四边形PACB为正方形,圆心到直线y=k(x+1)的距离小于或等于PC=2
,即
≤2
,由此求得k的范围.
| 2 |
| |2k-0+k| | ||
|
| 2 |
解答:
解:∵C的方程为x2+y2-4x=0,故圆心为C(2,0),半径R=2.
设两个切点分别为A、B,则由题意可得四边形PACB为正方形,故有PC=
R=2
,
∴圆心到直线y=k(x+1)的距离小于或等于PC=2
,
即
≤2
,解得k2≤8,可得-2
≤k≤2
,
故选:B.
设两个切点分别为A、B,则由题意可得四边形PACB为正方形,故有PC=
| 2 |
| 2 |
∴圆心到直线y=k(x+1)的距离小于或等于PC=2
| 2 |
即
| |2k-0+k| | ||
|
| 2 |
| 2 |
| 2 |
故选:B.
点评:本题主要考查直线和圆相交的性质,点到直线的距离公式的应用,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
已知数列{an}对任意的m、n∈N*,满足am+n=am+an,且a2=1,那么a10等于( )
| A、3 | B、5 | C、7 | D、9 |
某几何体的三视图如图所示,则它的体积是( )


| A、5 | ||
| B、6 | ||
C、
| ||
D、
|
设全集U=R,M={x|x2+3x<0},N={x|y=
},则图中阴影部分表示的集合为( )
| -x-1 |

| A、{x|x>-1} |
| B、{x|-3<x<0} |
| C、{x|x≤-3} |
| D、{x|-1<x<0} |
已知等差数列{an}中,a3+a4=a12,a1+a2=10,则a2+a4+…a100的值等于( )
| A、1300 | ||
| B、1350 | ||
| C、2650 | ||
D、
|
已知函数f(x)=x2+mx+n(m,n∈R)的值域为[0,+∞),若关于x的不等式f(x)<a-1的解集为(m-3,m+2),则实数a的值是( )
A、
| ||
B、
| ||
| C、6 | ||
D、
|
已知复数z满足
=i(i为虚数单位),则z的虚部为( )
| 1+z |
| 1-z |
| A、1 | B、-i | C、i | D、-1 |
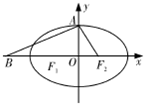 如图,设椭圆C:
如图,设椭圆C: