题目内容
已知函数f（x）=x2+mx+n（m，n∈R）的值域为[0，+∞），若关于x的不等式f（x）＜a-1的解集为（m-3，m+2），则实数a的值是（ ）
A、
| ||
B、
| ||
| C、6 | ||
D、
|
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：由已知可得△=m2-4n=0，①m-3+m+2=-m，②（m-3）（m+2）=n-a+1，③，联立可解．
解答：
解：∵函数f（x）=x2+mx+n（m，n∈R）的值域为[0，+∞），
∴△=m2-4n=0，①
又关于x的不等式f（x）＜a-1的解集为（m-3，m+2），
∴m-3和m+2为方程f（x）=a-1的两实根，
∴m-3+m+2=-m，②（m-3）（m+2）=n-a+1，③
由①②解得m=
，n=
，代入③可解得a=
故选：D
∴△=m2-4n=0，①
又关于x的不等式f（x）＜a-1的解集为（m-3，m+2），
∴m-3和m+2为方程f（x）=a-1的两实根，
∴m-3+m+2=-m，②（m-3）（m+2）=n-a+1，③
由①②解得m=
| 1 |
| 3 |
| 1 |
| 36 |
| 29 |
| 4 |
故选：D
点评：本题考查一元二次不等式的解法，涉及韦达定理的应用，属基础题．
练习册系列答案
相关题目
复数z=
-
的虚部为（ ）
| 1+i |
| i |
| i |
| 1+i |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
在△ABC中，AC=
，AB=3，BC=2，M，N，P分别为AC，AB，BC中点，将△ABC沿MN，NP，MP折起得到三棱锥S-MNP，三棱锥S-MNP外接球的表面积为（ ）
| 7 |
| A、10π | ||
| B、8π | ||
| C、5π | ||
D、
|
在平面直角坐标系xOy中，圆C的方程为x2+y2-4x=0．若直线y=k（x+1）上存在一点P，使过P所作的圆的两条切线相互垂直，则实数k的取值范围是（ ）
A、（-∞，-2
| ||||||||
B、[-2
| ||||||||
C、[-
| ||||||||
D、（-∞，-2
|
在区间[0，π]内随机取两个数分别记为a、b，则使得函数f（x）=x2+2ax-b2+π有零点的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
某程序框图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
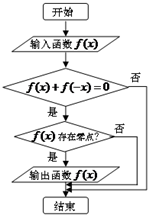
| A、f（x）=lnx | ||
B、f（x）=
| ||
| C、f（x）=ex | ||
| D、f（x）=x3 |
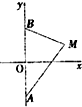已知点A、B的坐标分别是（0，-1），（0，1），直线AM、BM相交于点M，且它们的斜率之积为-