题目内容
已知平面向量
=（cosφ，sinφ），b=（cosx，sinx），其中0＜φ＜π，且函数f（x）=（
•
）cosx+sin（φ-x）sinx的图象过点（
，1）．
（Ⅰ）求φ的值；
（Ⅱ）将函数y=f（x）图象向右平移
，得到函数y=g（x）的图象，求函数y=g（x）递减区间．
| a |
| a |
| b |
| π |
| 6 |
（Ⅰ）求φ的值；
（Ⅱ）将函数y=f（x）图象向右平移
| π |
| 6 |
考点：三角函数中的恒等变换应用,平面向量数量积的运算,函数y=Asin（ωx+φ）的图象变换
专题：常规题型,三角函数的图像与性质
分析：（Ⅰ）代入向量数量积的坐标运算，利用和差公式化简，代入点（
，1），根据φ的范围求出φ的值；（Ⅱ）先根据图象平移求出g（x）的解析式，然后结合余弦函数的单调性求单调区间．
| π |
| 6 |
解答：
解：f（x）=（cosφcosx+sinφsinx）cosx+sin（φ-x）sinx
=cos（φ-x）cosx+sin（φ-x）sinx
=cos（φ-2x）
把点（
，1）代入得，cos（φ-2×
）=1
解得：φ=2kπ+
，
又∵0＜φ＜π，∴φ=
．
（Ⅱ）将函数y=f（x）图象向右平移
，得到函数y=cos[2（x-
）-
]=cos（2x-
）的图象．
∴g（x）=cos（2x-
），
由2kπ≤2x-
≤2kπ+π，得kπ+
≤x≤kπ+
（k∈Z），
∴函数y=g（x）递减区间为[kπ+
，kπ+
]（k∈Z）．
=cos（φ-x）cosx+sin（φ-x）sinx
=cos（φ-2x）
把点（
| π |
| 6 |
| π |
| 6 |
解得：φ=2kπ+
| π |
| 3 |
又∵0＜φ＜π，∴φ=
| π |
| 3 |
（Ⅱ）将函数y=f（x）图象向右平移
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
∴g（x）=cos（2x-
| 2π |
| 3 |
由2kπ≤2x-
| 2π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
∴函数y=g（x）递减区间为[kπ+
| π |
| 3 |
| 5π |
| 6 |
点评：本题考查了向量的数量积、三角变换与三角函数的图象与性质，解题的关键是利用公式化简，图象平移时左加右减，在自变量x上加上或减去一个常数．
练习册系列答案
相关题目
在平面直角坐标系xOy中，圆C的方程为x2+y2-4x=0．若直线y=k（x+1）上存在一点P，使过P所作的圆的两条切线相互垂直，则实数k的取值范围是（ ）
A、（-∞，-2
| ||||||||
B、[-2
| ||||||||
C、[-
| ||||||||
D、（-∞，-2
|
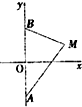已知点A、B的坐标分别是（0，-1），（0，1），直线AM、BM相交于点M，且它们的斜率之积为-