题目内容
已知数列{an}的前n项和为Sn,且2Sn=9-an,bn=3-2log3an.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)令cn=
,求数列{cn}的前n项和Tn;
(Ⅲ)证明:当n≥2时,a2nbn<1.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)令cn=
| b n |
| a n |
(Ⅲ)证明:当n≥2时,a2nbn<1.
考点:数列的求和,数列与函数的综合
专题:等差数列与等比数列
分析:(Ⅰ):由2Sn=9-an仿写出2Sn-1=9-an-1,两式相减得到an=
an-1(n≥2),判定出数列{an}是以3为首项,
为公比的等比数列,利用公式求出数列{an}和{bn}的通项公式;
(Ⅱ)由9Ⅰ)求出cn=
=
(2n-1)×3n,利用错位相减求出数列{cn}的前n项和Tn;
(Ⅲ)利用数列单调性的定义,判定出数列{a2nbn}为单调递减数列;求出数列的最大值为 a2b1,证明出不等式.
| 1 |
| 3 |
| 1 |
| 3 |
(Ⅱ)由9Ⅰ)求出cn=
| b n |
| a n |
| 1 |
| 9 |
(Ⅲ)利用数列单调性的定义,判定出数列{a2nbn}为单调递减数列;求出数列的最大值为 a2b1,证明出不等式.
解答:
解(Ⅰ):∵数列{an}的前n项和为Sn,且2Sn=9-an①,
∴n≥2时,2Sn-1=9-an-1②,
①-②得2an=-an+an-1(n≥2),
∴an=
an-1(n≥2)
又∵n=1时2S1=2a1=9-a1,
∴a1=3
∴数列{an}是以3为首项,
为公比的等比数列,
∴an=3•(
)n-1=32-n;
bn=3-2log3an=2n-1,
∴{bn}是首项为1,公差为2的等差数列.
∴an=32-n,bn=2n-1
(Ⅱ)∵cn=
=
(2n-1)×3n,
∴Tn=
[1×31+3×32+…+(2n-3)×3n-1+(2n-1)×3n]③
3Tn=
[1×32+3×33+…+(2n-3)×3n+(2n-1)×3n+1]④
③-④得-2Tn=
[1×3+2(32+33+…+3n)-(2n-1)×3n+1]
=
[3+
-(2n-1)×3n+1]
=
[(2-2n)3n-2]
∴Tn=(n-1)•3n-1+
(Ⅲ)证明:由(Ⅰ)知a2nbn=9×(
)2n×(2n-1)
∵a2(n+1)bn+1-a2nbn=9(
)2n+2×(2n+1)-9(
)2n×(2n-1)=(
)2n(10-16n)<0
∴数列{a2nbn}为单调递减数列;
∴当n≥2时,a2nbn<a2b1=1即当n≥2时,a2nbn<1.
∴n≥2时,2Sn-1=9-an-1②,
①-②得2an=-an+an-1(n≥2),
∴an=
| 1 |
| 3 |
又∵n=1时2S1=2a1=9-a1,
∴a1=3
∴数列{an}是以3为首项,
| 1 |
| 3 |
∴an=3•(
| 1 |
| 3 |
bn=3-2log3an=2n-1,
∴{bn}是首项为1,公差为2的等差数列.
∴an=32-n,bn=2n-1
(Ⅱ)∵cn=
| b n |
| a n |
| 1 |
| 9 |
∴Tn=
| 1 |
| 9 |
3Tn=
| 1 |
| 9 |
③-④得-2Tn=
| 1 |
| 9 |
=
| 1 |
| 9 |
| 18(1-3n-1) |
| 1-3 |
=
| 1 |
| 3 |
∴Tn=(n-1)•3n-1+
| 1 |
| 3 |
(Ⅲ)证明:由(Ⅰ)知a2nbn=9×(
| 1 |
| 3 |
∵a2(n+1)bn+1-a2nbn=9(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴数列{a2nbn}为单调递减数列;
∴当n≥2时,a2nbn<a2b1=1即当n≥2时,a2nbn<1.
点评:此题考查已知数列的递推关系求出数列的通项公式的知识点,属于中档题.准确运用等差、等比数列的通项与求和公式,利用错位相减法求和,是解决本题的关键.

练习册系列答案
相关题目
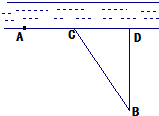 甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,
甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,