题目内容
19.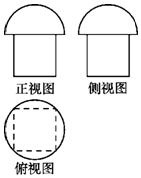 一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{2\sqrt{2}π}}{3}$ | C. | $8+\frac{{4\sqrt{2}π}}{3}$ | D. | $8+\frac{{8\sqrt{2}π}}{3}$ |
分析 首先由几何体还原几何体,是下面是底面为正方体,上面是半径为$\sqrt{2}$的半球,由此计算体积.
解答 解:由几何体的三视图得到几何体为组合体,下面是底面为正方体,上面是半径为$\sqrt{2}$的半球,
所以几何体的体积为2×2×2+$\frac{1}{2}×\frac{4}{3}π×(\sqrt{2})^{3}$=8+$\frac{4\sqrt{2}π}{3}$
故选C.
点评 本题考查了组合体的三视图以及体积的计算;关键是明确几何体的形状,由体积公式计算.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
9.函数y=loga(x-3)+2(a>0,a≠1)的图象过定点P,且角α的终边过点P,则的值为sin2α+cos2α( )
| A. | $\frac{7}{5}$ | B. | $\frac{6}{5}$ | C. | 4 | D. | 5 |
7.已知函数f(x)=aln(x+1)-x2,若对?p,q∈(0,1),且p≠q,有$\frac{{f({p+1})-f({q+1})}}{p-q}>2$恒成立,则实数a的取值范围为( )
| A. | (-∞,18) | B. | (-∞,18] | C. | [18,+∞) | D. | (18,+∞) |
8.某几何体的三视图如图所示,则其体积为( )
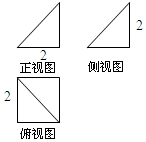

| A. | 4 | B. | $\frac{7}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |