题目内容
4．二项式${（x-\frac{1}{{\root{3}{x}}}）^8}$的展开式中，常数项是28．分析 利用通项公式即可得出．
解答 解：通项公式Tr+1=${∁}_{8}^{r}$x8-r$（-\frac{1}{\root{3}{x}}）^{r}$=（-1）r${∁}_{8}^{r}$${x}^{8-\frac{4r}{3}}$，
令8-$\frac{4r}{3}$=0，解得r=6．
∴常数项=${∁}_{8}^{6}$=28．
故答案为：28．
点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
14．如图所示，一个几何体的三视图中四边形均为边长为4的正方形，则这个几何体的体积为（ ）
| A． | $64-\frac{32π}{3}$ | B． | 64-16π | C． | $64-\frac{16π}{3}$ | D． | $64-\frac{8π}{3}$ |
12．某届奥运会上，中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二，某校体育爱好者在高三 年级一班至六班进行了“本届奥运会中国队表现”的满意度调查（结果只有“满意”和“不满意”两种），从被调查的学生中随机抽取了50人，具体的调查结果如表：
（1）在高三年级全体学生中随机抽取一名学生，由以上统计数据估计该生持满意态度的概率；
（2）若从一班至二班的调查对象中随机选取4人进行追踪调查，记选中的4人中对“本届奥运会中国队表现”不满意的人数为ξ，求随机变量ξ的分布列及数学期望．
| 班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
| 频数 | 5 | 9 | 11 | 9 | 7 | 9 |
| 满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
（2）若从一班至二班的调查对象中随机选取4人进行追踪调查，记选中的4人中对“本届奥运会中国队表现”不满意的人数为ξ，求随机变量ξ的分布列及数学期望．
19．
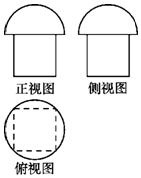一个几何体的三视图如图所示，其中正视图和侧视图相同，其上部分是半圆，下部分是边长为2的正方形；俯视图是边长为2的正方形及其外接圆．则该几何体的体积为（ ）
一个几何体的三视图如图所示，其中正视图和侧视图相同，其上部分是半圆，下部分是边长为2的正方形；俯视图是边长为2的正方形及其外接圆．则该几何体的体积为（ ）| A． | $4+\frac{2π}{3}$ | B． | $4+\frac{{2\sqrt{2}π}}{3}$ | C． | $8+\frac{{4\sqrt{2}π}}{3}$ | D． | $8+\frac{{8\sqrt{2}π}}{3}$ |
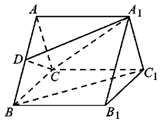如图，在三棱柱ABC-A1B1C1中，底面△ABC是等边三角形，侧面AA1B1B为正方形，且AA1⊥平面ABC，D为线段AB上的一点．