题目内容
10.已知直线l:$\left\{\begin{array}{l}x=2+tcosα\\ y=tsinα\end{array}$(t为参数),椭圆C:$\left\{\begin{array}{l}x=3cosϕ\\ y=\sqrt{5}sinϕ\end{array}$(φ为参数),F为椭圆C的右焦点.(1)当α=$\frac{π}{4}$时,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求直线l和曲线C的极坐标方程;
(2)设直线l与椭圆C交于A、B两点,求|FA|•|FB|的最大值与最小值.
分析 (1)利用三种方程的转化方法,求直线l和曲线C的极坐标方程;
(2)将直线l的参数方程代入椭圆C的普通方程,利用参数的几何意义,即可求|FA|•|FB|的最大值与最小值.
解答 解:(1)当α=$\frac{π}{4}$时,直线l:$\left\{\begin{array}{l}x=2+tcosα\\ y=tsinα\end{array}$的普通方程为x-y-2=0,极坐标方程为ρcosα-ρsinα-2=0;
椭圆C:$\left\{\begin{array}{l}x=3cosϕ\\ y=\sqrt{5}sinϕ\end{array}$(φ为参数)的普通方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1,极坐标方程为5ρ2cos2α+9ρ2sin2α=45.(5分)
(2)将直线l的参数方程代入椭圆C的普通方程,并整理得:(5+4sin2α)t2+20tcosα-25=0.
设点A,B在直线参数方程中对应的参数分别为t1,t2,则
|FA|•|FB|=|t1t2|=$\frac{25}{5+4si{n}^{2}α}$.
当sinα=0时,|FA|•|FB|取最大值5;
当sinα=±1时,|FA|•|FB|取最小值$\frac{25}{9}$.…(5分)
点评 本题考查参数方程化成普通方程,考查学生的计算能力,正确运用参数的几何意义是关键.

练习册系列答案
相关题目
20.已知0<a1<a2<a3,则使得${({1-{a_i}x})^2}<1({i=1,2,3})$都成立的x的取值范围是( )
| A. | $({0,\frac{1}{a_3}})$ | B. | $({0,\frac{2}{a_3}})$ | C. | $({0,\frac{1}{a_1}})$ | D. | $({0,\frac{2}{a_1}})$ |
2.已知全集U=R,集合M={x||x|<1},N={y|y=2x,x∈R},则集合∁U(M∪N)等于( )
| A. | (-∞,-1] | B. | (-1,2) | C. | (-∞,-1]∪[2,+∞) | D. | [2,+∞) |
19.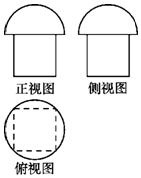 一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
 一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和侧视图相同,其上部分是半圆,下部分是边长为2的正方形;俯视图是边长为2的正方形及其外接圆.则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{2\sqrt{2}π}}{3}$ | C. | $8+\frac{{4\sqrt{2}π}}{3}$ | D. | $8+\frac{{8\sqrt{2}π}}{3}$ |
20.若函数$f(x)=\left\{\begin{array}{l}cosx,x≤a\\ \frac{1}{x},x>a\end{array}\right.$的值域为[-1,1],则实数a的取值范围是( )
| A. | [1,+∞) | B. | (-∞,-1] | C. | (0,1] | D. | (-1,0) |