题目内容
甲、乙等6人按下列要求站成一排,分别有多少不同的站法?
(1)甲不站在两端;
(2)甲、乙之间恰好相隔两人;
(3)甲不站在最左边,乙不站在最右边.
(1)甲不站在两端;
(2)甲、乙之间恰好相隔两人;
(3)甲不站在最左边,乙不站在最右边.
考点:计数原理的应用
专题:应用题,排列组合
分析:(1)甲不站在两端,先安排甲,有
=4种方法,再安排其余5人;
(2)选两人站在甲、乙之间,作为整体,再与其余2人全排;
(3)先全排,再减去不符合要求的情况.
| C | 1 4 |
(2)选两人站在甲、乙之间,作为整体,再与其余2人全排;
(3)先全排,再减去不符合要求的情况.
解答:
解:(1)甲不站在两端,先安排甲,有
=4种方法,再安排其余5人,共有4
=480种方法;
(2)选两人站在甲、乙之间,作为整体,再与其余2人全排,共有
=144种方法;
(3)先全排,再减去不符合要求的情况,共有
-2
+
=504种方法.
| C | 1 4 |
| A | 5 5 |
(2)选两人站在甲、乙之间,作为整体,再与其余2人全排,共有
| C | 2 4 |
| A | 2 2 |
| A | 2 2 |
| A | 3 3 |
(3)先全排,再减去不符合要求的情况,共有
| A | 6 6 |
| A | 5 5 |
| A | 4 4 |
点评:本题考查排列知识,先根据已知找到突破口,再以此推出其它位置的人是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
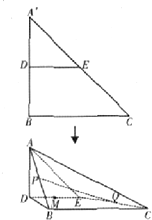 如图,在Rt△A′BC中,A′B=BC=2,D,E分别是A′B,A′C的中点,将△A′DE沿线段DE折起到△ADE,使平面ADE⊥平面DBCE.
如图,在Rt△A′BC中,A′B=BC=2,D,E分别是A′B,A′C的中点,将△A′DE沿线段DE折起到△ADE,使平面ADE⊥平面DBCE. 过x轴上动点A(a,0),引抛物线y=x2+3的两条切线AP、AQ,切点分别为P、Q.
过x轴上动点A(a,0),引抛物线y=x2+3的两条切线AP、AQ,切点分别为P、Q. 如图所示的几何体为一简单组合体,其底面ABCD为菱形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
如图所示的几何体为一简单组合体,其底面ABCD为菱形,PD⊥平面ABCD,EC∥PD,且PD=2EC.