题目内容
 过x轴上动点A(a,0),引抛物线y=x2+3的两条切线AP、AQ,切点分别为P、Q.
过x轴上动点A(a,0),引抛物线y=x2+3的两条切线AP、AQ,切点分别为P、Q.(Ⅰ)若a=-1,求直线PQ的方程;
(Ⅱ)探究直线PQ是否经过定点,若有,请求出定点的坐标;否则,请说明理由.
考点:直线与圆锥曲线的综合问题,利用导数研究曲线上某点切线方程,直线的一般式方程
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(Ⅰ)利用函数的导数,通过切线的斜率相等,求出P,Q的坐标,然后求直线PQ的方程;
(Ⅱ)(先猜后证)猜测直线PQ过定点(0,6),证明如下:
过A(a,0)的直线方程为y-0=k(x-a),联立直线与抛物线方程,通过韦达定理推出PQ的方程,然后说明直线PQ过定点(0,6).
(Ⅱ)(先猜后证)猜测直线PQ过定点(0,6),证明如下:
过A(a,0)的直线方程为y-0=k(x-a),联立直线与抛物线方程,通过韦达定理推出PQ的方程,然后说明直线PQ过定点(0,6).
解答:
解:(Ⅰ)∵y'=(x2+3)′=2x------(1分)
不妨设Q(x1,x12+3),P(x2,x22+3),x1<x2
∴kAQ=
=2x1,kAP=
=2x2-------(3分)
x12+3=2x12+2x1⇒x12+2x1-3=0⇒x1=1,x2=-3,
∴P(1,4),Q(-3,12),
由两点式可得?PQ:2x+y-6=0-----------(6分)
(Ⅱ)(先猜后证)令a=0,依(Ⅰ)步骤可求得直线PQ:y=6
联立
得交点(0,6),故猜测直线PQ过定点(0,6)-----(7分)
证明如下:
过A(a,0)的直线方程为y-0=k(x-a)
⇒x2+3=kx-ka,
x2-kx+ka+3=0△=k2-4(ka+3)=0,k2-4ka-12=0
∴k1k2=-12,即2x1•2x2=-12,
∴x1x2=-3------(9分)
设Q(x1,x12+3),P(x2,x22+3)
?PQ:y-x12-3=
(x-x1)⇒y-x12-3=(x2+x1)(x-x1)
令x=0,y=-x2x1-x12+x12+3=3-x1x2=3+3=6,
即直线PQ过定点(0,6)----(12分)
不妨设Q(x1,x12+3),P(x2,x22+3),x1<x2
∴kAQ=
| x12+3 |
| x1+1 |
| x22+3 |
| x2+1 |
x12+3=2x12+2x1⇒x12+2x1-3=0⇒x1=1,x2=-3,
∴P(1,4),Q(-3,12),
由两点式可得?PQ:2x+y-6=0-----------(6分)
(Ⅱ)(先猜后证)令a=0,依(Ⅰ)步骤可求得直线PQ:y=6
联立
|
证明如下:
过A(a,0)的直线方程为y-0=k(x-a)
|
x2-kx+ka+3=0△=k2-4(ka+3)=0,k2-4ka-12=0
∴k1k2=-12,即2x1•2x2=-12,
∴x1x2=-3------(9分)
设Q(x1,x12+3),P(x2,x22+3)
?PQ:y-x12-3=
| x22+3-x12-3 |
| x2-x1 |
令x=0,y=-x2x1-x12+x12+3=3-x1x2=3+3=6,
即直线PQ过定点(0,6)----(12分)
点评:本题考查直线与抛物线的位置关系,圆锥曲线方程的综合应用,函数的导数以及切线方程的应用,难度比较大的压轴题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
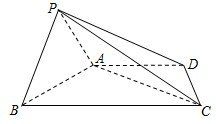 如图,四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,
如图,四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC, 在平面直角坐标系中,已知椭圆C:
在平面直角坐标系中,已知椭圆C: