题目内容
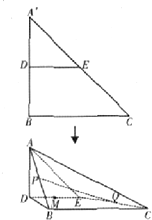 如图,在Rt△A′BC中,A′B=BC=2,D,E分别是A′B,A′C的中点,将△A′DE沿线段DE折起到△ADE,使平面ADE⊥平面DBCE.
如图,在Rt△A′BC中,A′B=BC=2,D,E分别是A′B,A′C的中点,将△A′DE沿线段DE折起到△ADE,使平面ADE⊥平面DBCE.(Ⅰ)若P,Q分别为AB,EC的中点,证明PQ∥平面AED.
(Ⅱ)若M为DE的中点,求三棱锥E-PMC的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)要证明PQ∥平面AED,过PQ构造一个平面与平面AED平行,取BD中点N,连接PN,NQ,得到平面平面PNQ∥平面ADE;
(Ⅱ)把求三棱锥E-PMC的体积转化成求三棱锥P-MEC的体积.
(Ⅱ)把求三棱锥E-PMC的体积转化成求三棱锥P-MEC的体积.
解答:
解:(Ⅰ)证明:如图取BD中点N,连接PN,NQ,
显然PN,NQ分别是△ABD,梯形BCED的中位线,
于是PN∥AD,NQ∥DE,PN?平面ADE,
∴PN∥平面ADE,NQ∥平面ADE,
又PN∩NQ=N,
因此平面PNQ∥平面ADE,
∴PQ∥平面AED.
(Ⅱ)易知DE∥BC,故∠ADE=∠A′DE=∠A′BC=90°,即AD⊥DE,
又因为平面ADE⊥平面DBCE,AD?平面ADE,
所以AD⊥平面DBCE
又PN∥AD,故PN即为三棱锥P-MEC的高,
由题意,易求得PN=
AD=
,BD=1,ME=
,
于是VE-PMC=VP-EMC=
×PN×
×ME×BD=
.

显然PN,NQ分别是△ABD,梯形BCED的中位线,
于是PN∥AD,NQ∥DE,PN?平面ADE,
∴PN∥平面ADE,NQ∥平面ADE,
又PN∩NQ=N,
因此平面PNQ∥平面ADE,
∴PQ∥平面AED.
(Ⅱ)易知DE∥BC,故∠ADE=∠A′DE=∠A′BC=90°,即AD⊥DE,
又因为平面ADE⊥平面DBCE,AD?平面ADE,
所以AD⊥平面DBCE
又PN∥AD,故PN即为三棱锥P-MEC的高,
由题意,易求得PN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
于是VE-PMC=VP-EMC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 24 |

点评:本题考查了线面位置关系的证明及几何体的体积,证明线面平行可以转化成证明面面平行;求三棱锥的体积关键是通过转换顶点转化成易求底面积和高的三棱锥的体积问题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
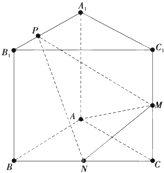 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且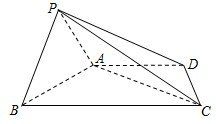 如图,四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,
如图,四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC, 在平面直角坐标系中,已知椭圆C:
在平面直角坐标系中,已知椭圆C: