题目内容
若a为大于零的常数,求函数f(x)=(a+sinx)(a+cosx)的值域.
考点:函数的值域
专题:
分析:将函数f(x)=(a+sinx)(a+cosx)展开,再进行三角换元即可.
解答:
解:f(x)=(a+sinx)(a+cosx)=a2+a(sinx+cosx)+sinxcosx
令sinx+cosx=t,则sinxcosx=
,t∈[-
,+
],所以原函数化为y=
(t-a)2+
,t∈[-
,
]
∴t=a是对称轴,对a进行分类讨论:
①当a∈(0,
)时,函数值域为[y(a),y(-
)],即y∈(
,a2+
a+
)
②当a∈[
,+∞)时,函数在[-
,
]上单调递减,故值域为[y(
),y(-
)],即y∈(a2-
a+
,a2+
a+
).
令sinx+cosx=t,则sinxcosx=
| t2-1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| a2-1 |
| 2 |
| 2 |
| 2 |
∴t=a是对称轴,对a进行分类讨论:
①当a∈(0,
| 2 |
| 2 |
| a2-1 |
| 2 |
| 2 |
| 1 |
| 2 |
②当a∈[
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
点评:本题考查含有字母的函数值域的求法,要注意字母的范围以及变量的取值范围,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
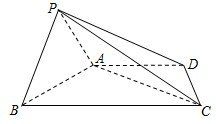 如图,四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,
如图,四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,