题目内容
已知x,y满足
则
的取值范围是 .
|
| y-2 |
| x-4 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,设z=
,利用z的几何意义,即可得到结论.
| y-2 |
| x-4 |
解答:
解:不等式组对应的平面区域如图: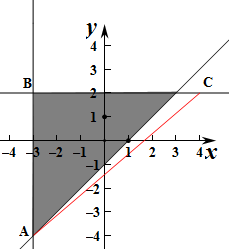
设z=
,则z的几何意义为P(x,y)到定点C(4,2)的斜率,
由图象可知当点P位于B时,此时直线CB的斜率最小为0,
当点P位于A时,此时直线AC的斜率最大,
由
,解得
,即A(-3,-4),
此时对应的z=
=
,
故0≤z≤
,
故答案为:[0,
]

设z=
| y-2 |
| x-4 |
由图象可知当点P位于B时,此时直线CB的斜率最小为0,
当点P位于A时,此时直线AC的斜率最大,
由
|
|
此时对应的z=
| -4-2 |
| -3-4 |
| 6 |
| 7 |
故0≤z≤
| 6 |
| 7 |
故答案为:[0,
| 6 |
| 7 |
点评:本题主要考查线性规划的应用,根据z的几何意义是解决本题的关键,要求熟练掌握斜率公式的计算.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
已知变量x,y满足约束条件
,则z=x+y的最大值为( )
|
| A、3 | B、4 | C、5 | D、6 |
(x2-x+1)10展开式中x3项的系数为( )
| A、-210 | B、210 |
| C、30 | D、-30 |
已知α是平面,m,n是直线,且m⊥α,则下列命题不正确的是( )
| A、若m∥n,则n⊥a |
| B、若n⊥α,则m∥n |
| C、若n∥α,则m⊥n |
| D、若m⊥n,则n∥α |
已知三点A(2,1),B(1,-2),C(
,-
),动点P(a,b)满足0≤
•
≤2,且0≤
•
≤2,则动点P到点C的距离小于
的概率为( )
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 5 |
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
 (文科)如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M、N分别是AD、BE的中点,将△ADE沿AE折起(D不在平面ABC内).下列说法正确的是
(文科)如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M、N分别是AD、BE的中点,将△ADE沿AE折起(D不在平面ABC内).下列说法正确的是