题目内容
（文科）如图，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M、N分别是AD、BE的中点，将△ADE沿AE折起（D不在平面ABC内）．下列说法正确的是①不论D折至何位置都有MN∥平面DEC；
②不论D折至何位置都有MN⊥AE；
③不论D折至何位置都有MN∥AB；
④在折起过程中，一定存在某个位置，使EC⊥AD；
⑤在折起过程中，一定存在某个位置，使MN∥BD．
考点：空间中直线与平面之间的位置关系
专题：开放型,空间位置关系与距离
分析：利用直线和平面平行、直线和平面垂直的判定定理、性质定理，结合反例、反证法的思想方法，逐一判断得出答案．
解答：
解：由已知，在未折叠的原梯形中，AB∥DE，BE∥AD．
∴四边形ABED为平行四边形，∴DA=EB．
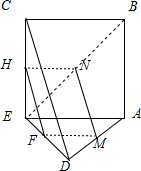
折叠后得出图形如下：
①过M，N分别作AE，BC的平行线，交ED，EC于F，H．连接FH
则
=
，
=
，
∵AM=BN，∴EN=DM，等量代换后得出HN=FM，
又CB∥EA，∴HN∥FM，
∴四边形MNHF是平行四边形．
∴MN∥FH
∵MN?面CED，HF?面CED．∴MN∥平面DEC． ①正确
②由已知，AE⊥ED，AE⊥EC，∴AE⊥面CED，HF?面CED，
∴AE⊥HF，∴MN⊥AE；②正确
③MN与AB 异面．假若MN∥AB，则MN与AB确定平面MNAB，
从而BE?平面MNAB，AD?平面MNAB．与BE和AD是异面直线矛盾．③错误．
④当CE⊥ED时，EC⊥AD．∵CE⊥EA，EA∩ED=E，∴CE⊥面AED，AD?面AED．得出EC⊥AD．④正确．
⑤由①知，在折起过程中，不存在某个位置，使MN∥BD．⑤错误．
故答案为：①②④．
解：由已知，在未折叠的原梯形中，AB∥DE，BE∥AD．∴四边形ABED为平行四边形，∴DA=EB．
折叠后得出图形如下：
①过M，N分别作AE，BC的平行线，交ED，EC于F，H．连接FH
则
| HN |
| CB |
| EN |
| EB |
| FM |
| EA |
| DM |
| DA |
∵AM=BN，∴EN=DM，等量代换后得出HN=FM，
又CB∥EA，∴HN∥FM，
∴四边形MNHF是平行四边形．
∴MN∥FH
∵MN?面CED，HF?面CED．∴MN∥平面DEC． ①正确
②由已知，AE⊥ED，AE⊥EC，∴AE⊥面CED，HF?面CED，
∴AE⊥HF，∴MN⊥AE；②正确
③MN与AB 异面．假若MN∥AB，则MN与AB确定平面MNAB，
从而BE?平面MNAB，AD?平面MNAB．与BE和AD是异面直线矛盾．③错误．
④当CE⊥ED时，EC⊥AD．∵CE⊥EA，EA∩ED=E，∴CE⊥面AED，AD?面AED．得出EC⊥AD．④正确．
⑤由①知，在折起过程中，不存在某个位置，使MN∥BD．⑤错误．
故答案为：①②④．
点评：本题考查空间直线和直线、直线和平面位置关系的判断．利用有关的定义、定理、性质确定命题的正确性，结合反例、反证法说明命题的错误性，是判断命题真假的常用方法．
练习册系列答案
相关题目
集合A={x|1＜x＜3}，B={x|x≤2}，则A∩B=（ ）
| A、{x|x＜3} |
| B、{x|2≤x＜3} |
| C、{x|1＜x≤2} |
| D、{x|1＜x＜2} |