题目内容
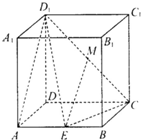在长方体ABCD-A1B1C1D1中，AD=1，AA1=AB=2．点E是线段AB上的动点，点M为D1C的中点．（1）当E点是AB中点时，求证：直线ME∥平面ADD1A1；
（2）若二面角A-D1E-C的余弦值为
4
| ||
| 15 |
考点：用空间向量求平面间的夹角,直线与平面平行的判定,与二面角有关的立体几何综合题
专题：空间位置关系与距离,空间向量及应用
分析：（1）取DD1的中点N，连结MN，AN，ME，由已知条件推导出四边形MNAE为平行四边形，由此能证明直线ME∥平面ADD1A1．
（2）设AE=m，以DA为x轴，以DC为y轴，以DD1为z轴，建立空间直角坐标系，结合题设条件利用向量法能求出线段AE的长．
（2）设AE=m，以DA为x轴，以DC为y轴，以DD1为z轴，建立空间直角坐标系，结合题设条件利用向量法能求出线段AE的长．
解答：
（1）证明：取DD1的中点N，连结MN，AN，ME，
∵点M为D1C的中点，E点是AB中点，
∴MN
CD，AE
CD，
∴四边形MNAE为平行四边形，
∴ME∥AN，
∵AN?平面ADD1A1，ME不包含于平面ADD1A1，
∴直线ME∥平面ADD1A1．
（2）解：设AE=m，如图以DA为x轴，以DC为y轴，以DD1为z轴，建立空间直角坐标系，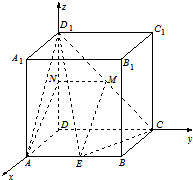
由题意知A（1，0，0），E（1，m，0），C（0，2，0），D1（0，0，2），
∴
=（-1，0，2），
=（0，m，0），
=（0，2，-2），
=(-1，2-m，0)，
设平面AD1E的法向量为
=(x1，y1，z1)，
则
•
=0，
•
=0，
∴
，∴
=(2，0，1)，
设平面D1EC的法向量为
=（x，y，z），
则
•
=0，
•
=0，
∴
，∴
=（2-m，1，1），
设二面角A-D1E-C的平面角为θ，
∵二面角A-D1E-C的余弦值为
，
∴cosθ=
=
，
整理，得20m2-116m+129=0，
解得m=
或m=
（舍），
∴线段AE的长为
．
∵点M为D1C的中点，E点是AB中点，
∴MN
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∴四边形MNAE为平行四边形，
∴ME∥AN，
∵AN?平面ADD1A1，ME不包含于平面ADD1A1，
∴直线ME∥平面ADD1A1．
（2）解：设AE=m，如图以DA为x轴，以DC为y轴，以DD1为z轴，建立空间直角坐标系，
由题意知A（1，0，0），E（1，m，0），C（0，2，0），D1（0，0，2），
∴
| AD1 |
| AE |
| D1C |
| EC |
设平面AD1E的法向量为
| n1 |
则
| n1 |
| AD1 |
| n1 |
| AE |
∴
|
| n1 |
设平面D1EC的法向量为
| n2 |
则
| n2 |
| D1C |
| n2 |
| EC |
∴
|
| n2 |
设二面角A-D1E-C的平面角为θ，
∵二面角A-D1E-C的余弦值为
4
| ||
| 15 |
∴cosθ=
| 5-2m | ||||
|
4
| ||
| 15 |
整理，得20m2-116m+129=0，
解得m=
| 3 |
| 2 |
| 43 |
| 10 |
∴线段AE的长为
| 3 |
| 2 |
点评：本题考查直线与平面平行的证明，考查线段落长的求法，是中档题，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，已知在四面体ABCD中，AB⊥BD，△ABC与△BCD是两个全等的等腰直角三角形，AB=BC=CD．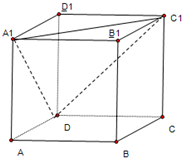
在正方体ABCD-A1B1C1D1中，求平面A1DC1与平面ADD1A1所成角的正切值．
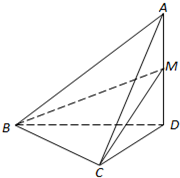如图，在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2
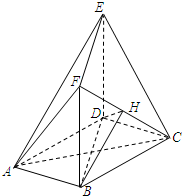如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，H是CF的中点．
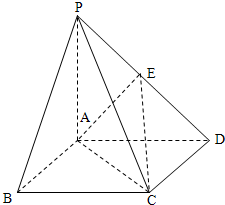如图，在四棱锥P-ABCD中，四边形ABCD为正方形，PA⊥面ABCD，且PA=AB=4，E为PD中点．
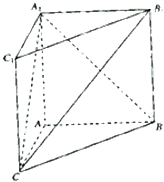如图，在直三棱柱ABC-A1B1C1中，