题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,已知b2=a(a+b),cos(A-B)+cosC=1-cos2C,试求
的值.
| a+c |
| b |
考点:正弦定理
专题:计算题,解三角形
分析:根据三角恒等变换公式,算出2sinAsinB=2sin2C,结合正弦定理得到ab=c2,代入b2=a(a+b)化简得出b2=a2+c2,可得△ABC是以B为直角的直角三角形.再根据勾股定理加以计算,即可得出
的值.
| a+c |
| b |
解答:
解:∵cos(A-B)=cosAcosB+sinAsinB,cosC=-cos(A+B)=-cosAcosB+sinAsinB,
∴cos(A-B)+cosC=2sinAsinB,
又∵cos(A-B)+cosC=1-cos2C=2sin2C,
∴2sinAsinB=2sin2C,结合正弦定理得ab=c2,
∵b2=a(a+b)=a2+ab,
∴b2=a2+c2,可得△ABC是以B为直角的直角三角形.
∵c2=ab=b2-a2,
∴(
)2+
-1=0,
=
(负值舍去),
∴
=
=
,
∴
=
+
.
∴cos(A-B)+cosC=2sinAsinB,
又∵cos(A-B)+cosC=1-cos2C=2sin2C,
∴2sinAsinB=2sin2C,结合正弦定理得ab=c2,
∵b2=a(a+b)=a2+ab,
∴b2=a2+c2,可得△ABC是以B为直角的直角三角形.
∵c2=ab=b2-a2,
∴(
| a |
| b |
| a |
| b |
| a |
| b |
| ||
| 2 |
∴
| c |
| b |
1-(
|
|
∴
| a+c |
| b |
| ||
| 2 |
|
点评:本题给出三角形ABC的边与角满足的条件,求边之间的比值.着重考查了三角恒等变换、正弦定理、勾股定理的应用等知识,属于中档题.

练习册系列答案
相关题目
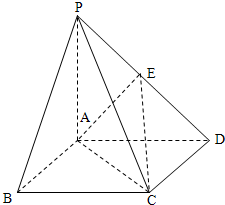 如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥面ABCD,且PA=AB=4,E为PD中点.
如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥面ABCD,且PA=AB=4,E为PD中点.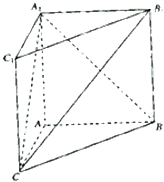 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,