题目内容
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 |
| B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
| C、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
| D、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.利用f′(x0)=0是x0为函数f(x)极值点的必要而不充分条件,即可判断出.
B.利用特称命题的否定是全称命题即可得出;
C.利用三角形的内角和定理、正弦余弦函数的单调性、和差化积即可得出.
D.利用偶函数的定义即可判断出.
B.利用特称命题的否定是全称命题即可得出;
C.利用三角形的内角和定理、正弦余弦函数的单调性、和差化积即可得出.
D.利用偶函数的定义即可判断出.
解答:
解:A.函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件,错误.
导数为零的点不一定为极值点,例如函数f(x)=x3,而f′(0)=0,但是此函数单调递增,无极值点;
B.命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1≥0”,因此B不正确;
C.命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为“在△ABC中,若sinA>sinB,则A>B”是真命题;其原因如下:∵0<B<A<A+B<π,∴0<
<
,0<
<
.
∴cos
>0,sin
>0.
∴sinA-sinB=2cos
sin
>0,即sinA>sinB.
D.“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件,正确.
其原因如下:函数f(x)=ax2+bx+c是偶函数?f(-x)=f(x)?2bx=0对于?x∈R都成立?b=0.
故选D
导数为零的点不一定为极值点,例如函数f(x)=x3,而f′(0)=0,但是此函数单调递增,无极值点;
B.命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1≥0”,因此B不正确;
C.命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为“在△ABC中,若sinA>sinB,则A>B”是真命题;其原因如下:∵0<B<A<A+B<π,∴0<
| A+B |
| 2 |
| π |
| 2 |
| A-B |
| 2 |
| π |
| 2 |
∴cos
| A+B |
| 2 |
| A-B |
| 2 |
∴sinA-sinB=2cos
| A+B |
| 2 |
| A-B |
| 2 |
D.“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件,正确.
其原因如下:函数f(x)=ax2+bx+c是偶函数?f(-x)=f(x)?2bx=0对于?x∈R都成立?b=0.
故选D
点评:本题综合考查了f′(x0)=0是x0为函数f(x)极值点的必要而不充分条件、特称命题的否定是全称命题、三角形的内角和定理、正弦余弦函数的单调性、和差化积、偶函数的定义等基础知识与基本技能方法,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
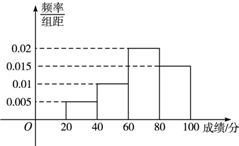 某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )| A、63 | B、65 | C、68 | D、70 |
△ABC的内角A,B,C所对的边为a,b,c;则下列命题正确的是( )
①若ab>c2;则C<
②若a+b>2c;则C<
③若a3+b3=c3;则C<
④若(a+b)c<2ab;则C>
.
①若ab>c2;则C<
| π |
| 3 |
②若a+b>2c;则C<
| π |
| 3 |
③若a3+b3=c3;则C<
| π |
| 2 |
④若(a+b)c<2ab;则C>
| π |
| 2 |
| A、②③④ | B、①②③ |
| C、①②④ | D、①③④ |
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
“a=2”是“关于x的不等式|x+1|+|x+2|<a的解集非空”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分又不必要条件 |
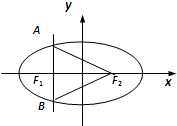 已知点F1、F2分别是椭圆
已知点F1、F2分别是椭圆