题目内容
边长为4的正四面体P-ABC中,E为PA的中点,则平面EBC与平面ABC所成锐二面角的余弦值为 .
考点:二面角的平面角及求法,与二面角有关的立体几何综合题
专题:综合题,空间角
分析:取BC的中点F,连接EF,AF,证明∠EFA为平面EBC与平面ABC所成锐二面角,求出△AEF的三边,即可求出平面EBC与平面ABC所成锐二面角的余弦值.
解答:
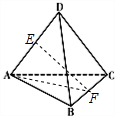 解:取BC的中点F,连接EF,AF,
解:取BC的中点F,连接EF,AF,
∵四面体P-ABC为正四面体,
∴EF⊥BC,AF⊥BC,
∴∠EFA为平面EBC与平面ABC所成锐二面角,
∵边长为4,E为PA的中点,
∴EA=2,AF=2
,EF⊥AP,
∴EF=
=2
,
∴cos∠EFA=
=
=
,
故答案为:
.
 解:取BC的中点F,连接EF,AF,
解:取BC的中点F,连接EF,AF,∵四面体P-ABC为正四面体,
∴EF⊥BC,AF⊥BC,
∴∠EFA为平面EBC与平面ABC所成锐二面角,
∵边长为4,E为PA的中点,
∴EA=2,AF=2
| 3 |
∴EF=
(2
|
| 2 |
∴cos∠EFA=
| EF |
| AF |
2
| ||
2
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查面面角,考查学生的计算能力,正确作出面面角是关键.

练习册系列答案
相关题目
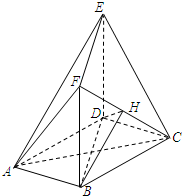 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.