题目内容
10.若函数y=f(x)的图象如图所示,则函数f(x)的解析式可以为( )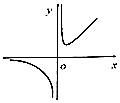
| A. | f(x)=$\frac{{2}^{x}+1}{x}$ | B. | f(x)=$\frac{ln({x}^{2}+2)}{x}$ | C. | f(x)=$\frac{{x}^{3}+3}{x}$ | D. | f(x)=$\frac{lnx}{x}$ |
分析 利用特殊点考查函数的单调性,奇偶性判断可得答案.
解答 解:根据图象可知:函数是非奇非偶函数,∴B排除.
函数图象在第三象限,x<0,∴D排除.
根据指数函数和幂函数的单调性:2x的图象比x3的图象平缓,∴A对.
故选A.
点评 本题考查了函数的图象的来判断函数f(x)的解析式,要综合利用图象的性质单调性,奇偶性判断.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
18.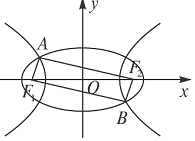 如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
 如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )| A. | $y=±\sqrt{2}x$ | B. | $y=±\frac{{\sqrt{2}}}{2}x$ | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{{\sqrt{6}}}{2}$x |
5.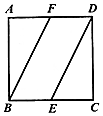 如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )
如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )
 如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )
如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )| A. | 点A与点C在某一位置可能重合 | B. | 点A与点C的最大距离为$\sqrt{3}$AB | ||
| C. | 直线AB与直线CD可能垂直 | D. | 直线AF与直线CE可能垂直 |
19.已知l是双曲线$C:\frac{x^2}{4}-\frac{y^2}{2}=1$的一条渐近线,P是l上的一点,F1,F2是C的两个焦点,若PF1⊥PF2,则△PF1F2的面积为( )
| A. | 12 | B. | $3\sqrt{2}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $2\sqrt{3}$ |
20.设偶函数f(x)满足f(x)=2-x-4(x≤0),则{x|f(x-2)>0}=( )
| A. | {x|x<-2或x>4} | B. | {x|x<-2或x>2} | C. | {x|x<0或x>4} | D. | {x|x<0或x>6} |
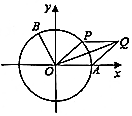 如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),∠AOB=α.
如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),∠AOB=α.