题目内容
15.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-(4a+1)x-8a+4,x<1}\\{lo{g}_{a}x,x≥1}\end{array}\right.$,若a=$\frac{1}{2}$,则函数f(x)的值域为R;若函数f(x)是R上的减函数,求实数a的取值范围为[$\frac{1}{4}$,$\frac{1}{3}$].分析 由题意利用函数的单调性的性质,对数函数、二次函数的单调性,可得$\left\{\begin{array}{l}{\frac{4a+1}{2}≥1}\\{0<a<1}\\{1-(4a+1)-8a+4≥0}\end{array}\right.$,由此求得实数a的取值范围.
解答 解:若a=$\frac{1}{2}$,当x<1时,函数f(x)=x2-3x=${(x-\frac{3}{2})}^{2}$-$\frac{9}{4}$∈[-2,+∞);
当x≥1时,f(x)=${log}_{\frac{1}{2}}x$≤0,故函数f(x)的值域为[-2,+∞)∪(-∞,0]=R.
若函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-(4a+1)x-8a+4,x<1}\\{lo{g}_{a}x,x≥1}\end{array}\right.$在R上单调递减,则$\left\{\begin{array}{l}{\frac{4a+1}{2}≥1}\\{0<a<1}\\{1-(4a+1)-8a+4≥0}\end{array}\right.$,
求得$\frac{1}{4}$≤a≤$\frac{1}{3}$,
故答案为:R;[$\frac{1}{4}$,$\frac{1}{3}$].
点评 本题主要考查函数的单调性的性质,对数函数、二次函数的单调性,属于中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
3.函数f(x)=1-ex的图象与x轴相交于点P,则曲线在点P处的切线的方程为( )
| A. | y=-e•x+1 | B. | y=-x+1 | C. | y=-x | D. | y=-e•x |
10.若函数y=f(x)的图象如图所示,则函数f(x)的解析式可以为( )
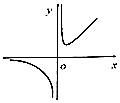

| A. | f(x)=$\frac{{2}^{x}+1}{x}$ | B. | f(x)=$\frac{ln({x}^{2}+2)}{x}$ | C. | f(x)=$\frac{{x}^{3}+3}{x}$ | D. | f(x)=$\frac{lnx}{x}$ |
7.已知四棱锥P-ABCD的底面为菱形,∠BAD=60°,侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法中错误的是( )
| A. | 异面直线PA与BC的夹角为60° | B. | 若M为AD的中点,则AD⊥平面PMB | ||
| C. | 二面角P-BC-A的大小为45° | D. | BD⊥平面PAC |
4.已知集合A={1,2,3,4},B={x|y=2x,y∈A},则A∩B=( )
| A. | {2} | B. | {1,2} | C. | {2,4} | D. | {1,2,4} |