题目内容
19.已知l是双曲线$C:\frac{x^2}{4}-\frac{y^2}{2}=1$的一条渐近线,P是l上的一点,F1,F2是C的两个焦点,若PF1⊥PF2,则△PF1F2的面积为( )| A. | 12 | B. | $3\sqrt{2}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $2\sqrt{3}$ |
分析 设P的坐标,利用PF1⊥PF2,建立方程,求出P的坐标,则△PF1F2的面积可求.
解答 解:由题意,设P($\sqrt{2}$y,y),
∵PF1⊥PF2,
∴(-$\sqrt{6}-\sqrt{2}$y,-y)•($\sqrt{6}-\sqrt{2}$y,-y)=0,
∴2y2-6+y2=0,∴|y|=$\sqrt{2}$,
∴△PF1F2的面积为$\frac{1}{2}•2\sqrt{6}•\sqrt{2}$=2$\sqrt{3}$.
故选D.
点评 本题考查双曲线的方程与性质,考查三角形面积的计算,比较基础.

练习册系列答案
相关题目
10.若函数y=f(x)的图象如图所示,则函数f(x)的解析式可以为( )
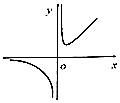

| A. | f(x)=$\frac{{2}^{x}+1}{x}$ | B. | f(x)=$\frac{ln({x}^{2}+2)}{x}$ | C. | f(x)=$\frac{{x}^{3}+3}{x}$ | D. | f(x)=$\frac{lnx}{x}$ |
7.已知四棱锥P-ABCD的底面为菱形,∠BAD=60°,侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法中错误的是( )
| A. | 异面直线PA与BC的夹角为60° | B. | 若M为AD的中点,则AD⊥平面PMB | ||
| C. | 二面角P-BC-A的大小为45° | D. | BD⊥平面PAC |
4.已知集合A={1,2,3,4},B={x|y=2x,y∈A},则A∩B=( )
| A. | {2} | B. | {1,2} | C. | {2,4} | D. | {1,2,4} |
11.设定义在R上的函数f(x)的导函数为f′(x),且满足f(2-x)=f(x),$\frac{f′(x)}{x-1}$<0,若x1+x2>2,x1<x2,则( )
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)与f(x2)的大小不能确定 |
9.设a1=3,${a_n}=\frac{1}{2}{a_{n-1}}+1(n≥2,n∈{N^*})$则数列{an}的通项公式是an=( )
| A. | $\frac{{{2^n}+1}}{{{2^{n-1}}}}$ | B. | $\frac{{{2^n}-1}}{{{2^{n-1}}}}$ | C. | $\frac{{{2^n}+1}}{{{2^{n+1}}}}$ | D. | $\frac{{{2^n}-1}}{{{2^{n+1}}}}$ |
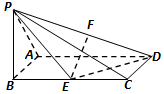 如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.
如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,且椭圆C过点$({1,\frac{3}{2}})$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,且椭圆C过点$({1,\frac{3}{2}})$.