题目内容
18.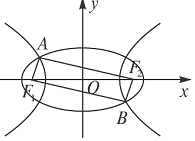 如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )| A. | $y=±\sqrt{2}x$ | B. | $y=±\frac{{\sqrt{2}}}{2}x$ | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{{\sqrt{6}}}{2}$x |
分析 由题意可知:AF1|+|AF2|=2a=4,丨AF1丨2+丨AF2丨2=丨F1F2丨2,则丨AF1丨=2-$\sqrt{2}$,丨AF2丨=2+$\sqrt{2}$,由双曲线的定义可知:2a′=|AF2|-|AF1|,c′=$\sqrt{3}$,b2=c2-a2=1,则双曲线C2的渐近线方程y=±$\frac{b}{a}$x.
解答 解:设|AF1|=x,|AF2|=y,
∵点A为椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$上的点,
∴2a=4,b=1,c=$\sqrt{3}$;
∴|AF1|+|AF2|=2a=4,即x+y=4;①
又四边形AF1BF2为矩形,
∴丨AF1丨2+丨AF2丨2=丨F1F2丨2,即x2+y2=(2c)2=12,②
由①②得 $\left\{\begin{array}{l}{x+y=4}\\{{x}^{2}+{y}^{2}=12}\end{array}\right.$,
解得:x=2-$\sqrt{2}$,y=2+$\sqrt{2}$,
设双曲线C2的实轴长为2a′,焦距为2c′,
则2a′=|AF2|-|AF1|=y-x=2$\sqrt{2}$,a=$\sqrt{2}$,
2c′=2$\sqrt{3}$,则c=$\sqrt{3}$,b2=c2-a2=1,
双曲线C2的渐近线方程y=±$\frac{b}{a}$x=±$\frac{\sqrt{2}}{2}$x,
故选B.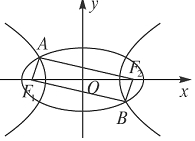
点评 本题考查双曲线的定义及简单几何性质,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
13.函数f(x)=$\frac{\sqrt{x-1}}{x-2}$的定义域为( )
| A. | (1,+∞) | B. | [1,+∞) | C. | [1,2) | D. | [1,2)∪(2,+∞) |
3.函数f(x)=1-ex的图象与x轴相交于点P,则曲线在点P处的切线的方程为( )
| A. | y=-e•x+1 | B. | y=-x+1 | C. | y=-x | D. | y=-e•x |
10.若函数y=f(x)的图象如图所示,则函数f(x)的解析式可以为( )
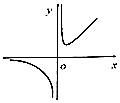

| A. | f(x)=$\frac{{2}^{x}+1}{x}$ | B. | f(x)=$\frac{ln({x}^{2}+2)}{x}$ | C. | f(x)=$\frac{{x}^{3}+3}{x}$ | D. | f(x)=$\frac{lnx}{x}$ |
7.已知四棱锥P-ABCD的底面为菱形,∠BAD=60°,侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法中错误的是( )
| A. | 异面直线PA与BC的夹角为60° | B. | 若M为AD的中点,则AD⊥平面PMB | ||
| C. | 二面角P-BC-A的大小为45° | D. | BD⊥平面PAC |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,且椭圆C过点$({1,\frac{3}{2}})$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,且椭圆C过点$({1,\frac{3}{2}})$.