题目内容
2.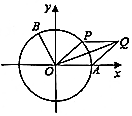 如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),∠AOB=α.
如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),∠AOB=α.(1)求$\frac{5cosα+6sinα}{4cosα-3sinα}$的值;
(2)设∠AOP=θ($\frac{π}{6}$≤θ≤$\frac{2π}{3}$),$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,四边形OAQP的面积为S,f(θ)=($\overrightarrow{OA}$•$\overrightarrow{OQ}$-$\frac{1}{2}$)2+2S2-$\frac{1}{2}$,求f(θ)的最值及此时θ的值.
分析 (1)依题意,可求得tanα=-2,将$\frac{5cosα+6sinα}{4cosα-3sinα}$中的“弦”化“切”即可求得其值;
(2)利用向量的数量积的坐标运算可求得f(θ)=(cosθ+$\frac{1}{2}$)2+2sin2θ-$\frac{1}{2}$=-(cosθ-$\frac{1}{2}$)2+2,利用-$\frac{1}{2}$≤cosθ≤$\frac{\sqrt{3}}{2}$,即可求得f(θ)的最值及此时θ的值.
解答 解:(1)依题意,tanα═-2,
∴$\frac{5cosα+6sinα}{4cosα-3sinα}$=$\frac{5+6tanα}{4-3tanα}$=-$\frac{7}{10}$;
(2)由已知点P的坐标为P(cosθ,sinθ),
又$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,|$\overrightarrow{OA}$=||$\overrightarrow{OP}$|,
∴四边形OAQP为菱形,
∴S=2S△OAP=sinθ,
∵A(1,0),P(cosθ,sinθ),
∴$\overrightarrow{OQ}$=(1+cosθ,sinθ),
∴$\overrightarrow{OA}$•$\overrightarrow{OQ}$=1+cosθ,
∴f(θ)=(cosθ+$\frac{1}{2}$)2+2sin2θ-$\frac{1}{2}$=-(cosθ-$\frac{1}{2}$)2+2
∵-$\frac{1}{2}$≤cosθ≤$\frac{\sqrt{3}}{2}$,
∴当cosθ=$\frac{1}{2}$,即θ=$\frac{π}{3}$时,f(θ)max=2;
当cosθ=-$\frac{1}{2}$,即θ=$\frac{2π}{3}$时,f(θ)min=1.
点评 本题考查三角函数的最值,着重考查三角函数中的恒等变换应用及向量的数量积的坐标运算,考查正弦函数的单调性及最值,属于中档题.

| A. | 若$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$,则$\vec b=\overrightarrow c$ | |
| B. | 若$\overrightarrow a•\overrightarrow b=0$,则$\vec a=\vec 0$或$\vec b=\vec 0$ | |
| C. | 若不平行的两个非零向量$\overrightarrow a,\overrightarrow b$满足$|\overrightarrow a|=|\overrightarrow b|$,则$(\overrightarrow a+\overrightarrow b)•(\overrightarrow a-\overrightarrow b)=0$ | |
| D. | 若$\overrightarrow a$与$\overrightarrow b$平行,则$\overrightarrow a•\overrightarrow b=|\overrightarrow a|•|\overrightarrow b|$ |
| A. | (1,+∞) | B. | [1,+∞) | C. | [1,2) | D. | [1,2)∪(2,+∞) |
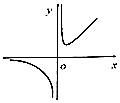
| A. | f(x)=$\frac{{2}^{x}+1}{x}$ | B. | f(x)=$\frac{ln({x}^{2}+2)}{x}$ | C. | f(x)=$\frac{{x}^{3}+3}{x}$ | D. | f(x)=$\frac{lnx}{x}$ |
| A. | 异面直线PA与BC的夹角为60° | B. | 若M为AD的中点,则AD⊥平面PMB | ||
| C. | 二面角P-BC-A的大小为45° | D. | BD⊥平面PAC |
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)与f(x2)的大小不能确定 |
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(千万元) | 2 | 3 | 3 | 4 | 5 |
(Ⅱ)当销售额为4(千万元)时,估计利润额的大小.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
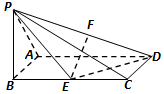 如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.
如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.