题目内容
20．设偶函数f（x）满足f（x）=2-x-4（x≤0），则{x|f（x-2）＞0}=（ ）| A． | {x|x＜-2或x＞4} | B． | {x|x＜-2或x＞2} | C． | {x|x＜0或x＞4} | D． | {x|x＜0或x＞6} |
分析 由偶函数f（x）满足f（x）=2-x-4（x≤0），可得f（x）=f（|x|）=2|x|-4，根据偶函数的性质将函数转化为绝对值函数，然后求解不等式可得答案．
解答 解：由偶函数f（x）满足f（x）=2-x-4（x≤0），故f（x）=f（|x|）=2|x|-4，
则f（x-2）=f（|x-2|）=2|x-2|-4，要使f（|x-2|）＞0，
只需2|x-2|-4＞0，|x-2|＞2，解得x＞4，或x＜0．
故解集为：{x|x＜0，或x＞4}．
故选：C．
点评 本题主要考查偶函数性质、不等式的解法以及相应的运算能力，解答本题的关键是利用偶函数的性质将函数转化为绝对值函数，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
10．若函数y=f（x）的图象如图所示，则函数f（x）的解析式可以为（ ）
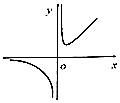
| A． | f（x）=$\frac{{2}^{x}+1}{x}$ | B． | f（x）=$\frac{ln（{x}^{2}+2）}{x}$ | C． | f（x）=$\frac{{x}^{3}+3}{x}$ | D． | f（x）=$\frac{lnx}{x}$ |
11．设定义在R上的函数f（x）的导函数为f′（x），且满足f（2-x）=f（x），$\frac{f′（x）}{x-1}$＜0，若x1+x2＞2，x1＜x2，则（ ）
| A． | f（x1）＜f（x2） | B． | f（x1）=f（x2） | ||
| C． | f（x1）＞f（x2） | D． | f（x1）与f（x2）的大小不能确定 |
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1，F2，抛物线y2=4x与椭圆C有相同的焦点，且椭圆C过点$（{1，\frac{3}{2}}）$．
15．
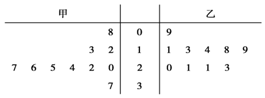某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个．命中个数的茎叶图如图，则下面结论中错误的一个是（ ）
某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个．命中个数的茎叶图如图，则下面结论中错误的一个是（ ）| A． | 乙的众数是21 | B． | 甲的中位数是24 | ||
| C． | 甲的极差是29 | D． | 甲罚球命中率比乙高 |
12．某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表：
（Ⅰ）用最小二乘法计算利润额y对销售额x的回归直线方程$\widehaty=\widehatbx+\widehata$；
（Ⅱ）当销售额为4（千万元）时，估计利润额的大小．
附：线性回归方程$\widehaty=\widehatbx+\widehata$中，$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$，$\widehata=\overline y-\widehatb\overline x$．
| 商店名称 | A | B | C | D | E |
| 销售额x（千万元） | 3 | 5 | 6 | 7 | 9 |
| 利润额y（千万元） | 2 | 3 | 3 | 4 | 5 |
（Ⅱ）当销售额为4（千万元）时，估计利润额的大小．
附：线性回归方程$\widehaty=\widehatbx+\widehata$中，$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$，$\widehata=\overline y-\widehatb\overline x$．
9．设a1=3，${a_n}=\frac{1}{2}{a_{n-1}}+1（n≥2，n∈{N^*}）$则数列{an}的通项公式是an=（ ）
| A． | $\frac{{{2^n}+1}}{{{2^{n-1}}}}$ | B． | $\frac{{{2^n}-1}}{{{2^{n-1}}}}$ | C． | $\frac{{{2^n}+1}}{{{2^{n+1}}}}$ | D． | $\frac{{{2^n}-1}}{{{2^{n+1}}}}$ |
10．要得到函数y=sin2x的图象，只需将函数y=cos（2x+$\frac{π}{6}$）的图象（ ）
| A． | 向右平移$\frac{π}{3}$个单位 | B． | 向左平移$\frac{π}{4}$个单位 | ||
| C． | 向左平移$\frac{π}{3}$个单位 | D． | 向右平移$\frac{π}{4}$个单位 |