题目内容
14.已知函数$f(x)=\sqrt{a{x^2}+bx}$满足:对于实数a的某些值,可以找到相应正数b,使得f(x)的定义域与值域相同,那么符合条件的实数a的个数是2.分析 由于函数解析式中,被开方式是一个类一元二次式,故我们可分a=0,a>0和a<0,三种情况,分别分析是否存在正实数b,使函数f(x)的定义域和值域相同,进而综合讨论结果,即可得到答案.
解答 解:(1)若a=0,则对于每个正数b,f(x)=$\sqrt{bx}$的定义域和值域都是[0,+∞)
故a=0满足条件.
(2)若a>0,则对于正数b,$f(x)=\sqrt{a{x^2}+bx}$的定义域为D=(-∞,-$\frac{b}{a}$]∪[0,+∞),
但f(x)的值域A⊆[0,+∞),故D≠A,即a>0不合条件;
(3)若a<0,则对正数b,定义域D=[0,-$\frac{b}{a}$],(f(x))max=$\frac{b}{2\sqrt{-a}}$,
f(x)的值域为[0,$\frac{b}{2\sqrt{-a}}$],则-$\frac{b}{a}$=$\frac{b}{2\sqrt{-a}}$?$\left\{\begin{array}{l}{a<0}\\{2\sqrt{-a}=-a}\end{array}\right.$.
综上所述:a的值为0或-4.
故答案为2.
点评 本题考查的知识点是函数的定义域及其求法,函数的值域,二次函数的图象和性质,其中熟练掌握一次函数和二次函数的图象和性质是解答本题的关键,解答中易忽略a=0时,也满足条件,而错解为a=-4.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
2.一直线l与平行四边形ABCD中的两边AB、AD分别交于E、F,且交其对角线AC于K,若$\overrightarrow{AB}$=2$\overrightarrow{AE}$,$\overrightarrow{AD}$=3$\overrightarrow{AF}$,$\overrightarrow{AC}$=λ$\overrightarrow{AK}$(λ∈R),则λ=( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 5 |
6.已知m>0,n>0,空间向量$\overrightarrow{a}$=(m,4,-3)与$\overrightarrow{b}$=(1,n,2)垂直,则mn的最大值为( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | 9、 | D. | $\frac{9}{4}$ |
4.函数y=sin(2x+$\frac{π}{3}$)的图象可以由函数y=sin2x的图象( )得到.
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
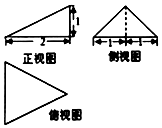 已知某三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2}{3}$,它的表面积为$2+2\sqrt{5}$.
已知某三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2}{3}$,它的表面积为$2+2\sqrt{5}$.