Question

5．由约束条件$\left\{\begin{array}{l}{x≥0，y≥0}\\{y≤-3x+3}\\{y≤kx+1}\end{array}\right.$，确定的可行域D能被半径为$\frac{\sqrt{2}}{2}$的圆面完全覆盖，则实数k的取值范围是$（-∞，\frac{1}{3}]$．

Answer 1

分析 先画出由约束条件确定的可行域D，由可行域能被圆覆盖得到可行域是封闭的，判断出直线y=kx+1斜率小于等于 $\frac{1}{3}$即可得出k的范围．

解答 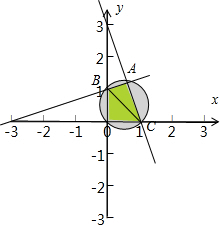解：∵可行域能被圆覆盖，
∴可行域是封闭的，
作出约束条件$\left\{\begin{array}{l}{x≥0，y≥0}\\{y≤-3x+3}\\{y≤kx+1}\end{array}\right.$的可行域：
可得B（0，1），C（1，0），|BC|=$\sqrt{2}$，
结合图，要使可行域能被$\frac{\sqrt{2}}{2}$为半径的圆覆盖，
只需直线y=kx+1与直线y=-3x+3的交点坐标在圆的内部，
两条直线垂直时，交点恰好在圆上，此时k=$\frac{1}{3}$，
则实数k的取值范围是：（-∞，$\frac{1}{3}$]．
故答案为：$（-∞，\frac{1}{3}]$．

点评 本题考查画不等式组表示的平面区域、考查将图形的大小关系转化为不等式．