Question

8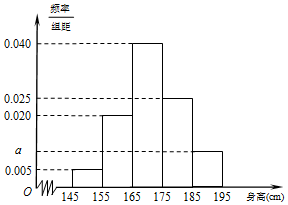．某中学随机选取了40名男生，将他们的身高作为样本进行统计，得到如图所示的频率分布直方图．观察图中数据，完成下列问题．
（Ⅰ）求a的值及样本中男生身高在[185，195]（单位：cm）的人数；
（Ⅱ）假设同一组中的每个数据可用该组区间的中点值代替，通过样本估计该校全体男生的平均身高；
（Ⅲ）在样本中，从身高在[145，155）和[185，195]（单位：cm）内的男生中任选两人，求这两人的身高都不低于185cm的概率．

Answer 1

分析 （Ⅰ）由题意，a=0.1-0.04-0.025-0.02-0.005=0.01，可得身高在[185，195]的频率为0.1，人数为4；
（Ⅱ）同一组中的每个数据可用该组区间的中点值代替，即可通过样本估计该校全体男生的平均身高；
（Ⅲ）求出基本事件的个数，即可求出概率．

解答 解：（Ⅰ）由题意，a=0.1-0.04-0.025-0.02-0.005=0.01，
身高在[185，195]的频率为0.1，人数为4；
（Ⅱ）估计该校全体男生的平均身高150×0.05+160×0.2+170×0.4+180×0.25+190×0.1=161.5；
（Ⅲ）在样本中，身高在[145，155）和[185，195]（单位：cm）内的男生分别有2人，4人，从身高在[145，155）和[185，195]（单位：cm）内的男生中任选两人，有${C}_{6}^{2}$=15种，这两人的身高都不低于185cm，有${C}_{4}^{2}$=6种，所以所求概率为$\frac{6}{15}$=0.4．

点评 本题考查频率分布直方图，考查概率的计算，考查学生读图的能力，属于中档题．