题目内容

16．在极坐标系中，圆ρ=2cosθ被直线ρcosθ=$\frac{1}{2}$所截得的弦长为$\sqrt{3}$．

分析 化直线和圆的极坐标方程为直角坐标方程，求出圆心到直线的距离为$\frac{1}{2}$，利用勾股定理求出截得的弦长．

解答 解：由ρcosθ=$\frac{1}{2}$，得x=$\frac{1}{2}$；
由ρ=2cosθ，得ρ2=2ρcosθ，即x2+y2-2x=0，圆心为（1，0），半径为1，
圆心到直线的距离为$\frac{1}{2}$，截得的弦长为2$\sqrt{1-\frac{1}{4}}$=$\sqrt{3}$，
故答案为：$\sqrt{3}$．

点评 本题考查了极坐标方程化直角坐标方程，考查了直线与圆的关系，是基础的计算题．

练习册系列答案
相关题目
6．已知O为△ABC的外心，且$\overrightarrow{BO}=λ\overrightarrow{BA}+μ\overrightarrow{BC}$．
①若∠C=90°，则λ+μ=$\frac{1}{2}$；
②若∠ABC=60°，则λ+μ的最大值为$\frac{2}{3}$．
7．已知P1（x1，y1），P2（x2，y2），P3（x3，y3），P4（x4，y4）是抛物线C：y2=8x上的点，F是抛物线C上的焦点，若|PF1|+|PF2|+|PF3|+|PF4|=20，则x1+x2+x3+x4等于（　　）
A．8B．10C．12D．16
4．已知向量$\overrightarrow a，\overrightarrow b$的夹角为120°，且$|\overrightarrow a|=1$，$|\overrightarrow b|=2$，则向量$\overrightarrow a+\overrightarrow b$在向量$\overrightarrow a$方向上的投影是（　　）
A．0B．$\frac{2}{3}$C．-1D．$\frac{1}{2}$
11．已知矩阵A=$[\begin{array}{l}{a}&{3}\\{2}&{d}\end{array}]$，若A$[\begin{array}{l}{1}\\{2}\end{array}]$=$[\begin{array}{l}{8}\\{4}\end{array}]$，求矩阵A的特征值．
1．已知椭圆W：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的上下顶点分别为A，B，且点B（0，-1）．F1，F2分别为椭圆W的左、右焦点，且∠F1BF2=120°．
（Ⅰ）求椭圆W的标准方程；
（Ⅱ）点M是椭圆上异于A，B的任意一点，过点M作MN⊥y轴于N，E为线段MN的中点．直线AE与直线y=-1交于点C，G为线段BC的中点，O为坐标原点．求∠OEG的大小．
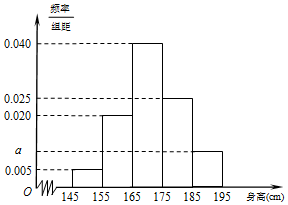8．某中学随机选取了40名男生，将他们的身高作为样本进行统计，得到如图所示的频率分布直方图．观察图中数据，完成下列问题．
（Ⅰ）求a的值及样本中男生身高在[185，195]（单位：cm）的人数；
（Ⅱ）假设同一组中的每个数据可用该组区间的中点值代替，通过样本估计该校全体男生的平均身高；
（Ⅲ）在样本中，从身高在[145，155）和[185，195]（单位：cm）内的男生中任选两人，求这两人的身高都不低于185cm的概率．
5．若双曲线x2+my2=2的虚轴长为2，则该双曲线的焦距为（　　）
A．2B．2$\sqrt{2}$C．2$\sqrt{3}$D．4
6．已知函数f（x）=x3-3a2x+2a2+1（a≥0）
（Ⅰ）求f（x）的单调区间；
（Ⅱ）讨论函数f（x）在区间（-2，3）内极值点的个数；
（Ⅲ）证明：当0≤x≤1时，f（x）+|1-a2|≥1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网