题目内容
20.已知向量$\overrightarrow{a}$=(2,-3),$\overrightarrow{b}$=(-3,x)且存在实数λ使$\overrightarrow{a}$=λ$\overrightarrow{b}$,那么|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\frac{\sqrt{13}}{2}$.分析 利用向量共线定理、模的计算公式即可得出.
解答 解:∵向量$\overrightarrow{a}$=(2,-3),$\overrightarrow{b}$=(-3,x)且存在实数λ使$\overrightarrow{a}$=λ$\overrightarrow{b}$,
∴-3×(-3)-2x=0,解得x=$\frac{9}{2}$.
2$\overrightarrow{a}$+$\overrightarrow{b}$=(1,-$\frac{3}{2}$).
那么|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{1}^{2}+(-\frac{3}{2})^{2}}$=$\frac{\sqrt{13}}{2}$.
故答案为:$\frac{\sqrt{13}}{2}$.
点评 本题考查了向量共线定理、模的计算公式、数量积运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
15.已知a,b∈R,i为虚数单位,若a+3i与2+bi在复平面内对应的点关于原点对称,则$\frac{a+bi}{1+i}$等于( )
| A. | -$\frac{5+i}{2}$ | B. | $\frac{-5+i}{2}$ | C. | $\frac{1+5i}{2}$ | D. | $\frac{1-5i}{2}$ |
5.若双曲线x2+my2=2的虚轴长为2,则该双曲线的焦距为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |
10.已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
| A. | a<b<c | B. | c<b<a | C. | a<c<b | D. | c<a<b |
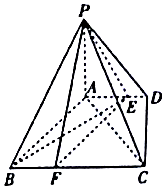 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.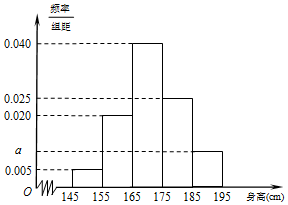 某中学随机选取了40名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.
某中学随机选取了40名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.