题目内容
18．已知sin（θ-$\frac{π}{4}$）=$\frac{\sqrt{3}}{3}$，则sin2θ=（ ）| A． | $\frac{1}{3}$ | B． | -$\frac{2}{3}$ | C． | $\frac{2\sqrt{5}}{5}$ | D． | -$\frac{2\sqrt{3}}{3}$ |
分析 由已知利用两角差的正弦函数公式，特殊角的三角函数值可求sinθ-cosθ=$\frac{\sqrt{6}}{3}$，两边平方，利用二倍角的正弦函数公式可求sin2θ的值．
解答 解：∵sin（θ-$\frac{π}{4}$）=$\frac{\sqrt{3}}{3}$，
∴$\frac{\sqrt{2}}{2}$（sinθ-cosθ）=$\frac{\sqrt{3}}{3}$，解得：sinθ-cosθ=$\frac{\sqrt{6}}{3}$，
∴两边平方可得：1-sin2θ=$\frac{2}{3}$，
∴sin2θ=$\frac{1}{3}$．
故选：A．
点评 本题主要考查了两角差的正弦函数公式，特殊角的三角函数值，二倍角的正弦函数公式在三角函数化简求值中的应用，考查了转化思想，属于基础题．
练习册系列答案
相关题目
8．
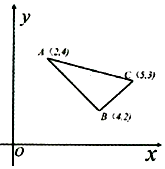已知点（x，y）在△ABC所包围的阴影区域内（包括边界），若有且仅有B（4，2）是使得z=ax-y取得最大值的最优解，则实数a的取值范围为（ ）
已知点（x，y）在△ABC所包围的阴影区域内（包括边界），若有且仅有B（4，2）是使得z=ax-y取得最大值的最优解，则实数a的取值范围为（ ）| A． | -1＜a＜1 | B． | -1≤a≤1 | C． | -1≤a＜1 | D． | -1＜a≤1 |
3．设Sn为等差数列{an}的前n项和，若a2017=S2017=2017，则首项a1=（ ）
| A． | -2014 | B． | -2015 | C． | -2016 | D． | -2017 |
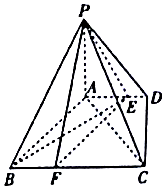如图，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，∠ADC=90°，AD∥BC，AB⊥AC，AB=AC=$\sqrt{2}$，点E在AD上，且AE=2ED．
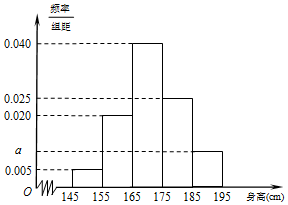某中学随机选取了40名男生，将他们的身高作为样本进行统计，得到如图所示的频率分布直方图．观察图中数据，完成下列问题．