题目内容
是否存在实数m,使得f(x)=-cos2x+2mcosx+m2+4m-3的最大值为3m,若存在,求出m的值;若不存在,请说明理由.
考点:复合三角函数的单调性
专题:三角函数的图像与性质
分析:将函数f(x)进行化简,利用换元法转化为一元二次函数即可得到结论.
解答:
解:f(x)=-(cosx-m)2+2m2+4m-3,
设t=cosx,则-1≤t≤1,
则函数等价为g(t)=-(t-m)2+2m2+4m-3,
假设存在满足条件的m.
ⅰ)当m≥1时,函数g(t)的最大值为g(1)=m2+6m-4,
令m2+6m-4=3m,得m=1(m=-4舍去),
ⅱ)当m≤-1时,函数g(t)的最大值为g(-1)=m2+2m-4,
令m2+2m-4=3m,得m=
(或m=
舍去)
ⅲ)当-1<m<1时,函数g(t)的最大值为g(m)=2m2+4m-3,
令2m2+4m-3=3m,得m=-
(舍去)m=1(舍去),
综上,存在m使得f(x)的最大值为3m.m=1或m=
.
设t=cosx,则-1≤t≤1,
则函数等价为g(t)=-(t-m)2+2m2+4m-3,
假设存在满足条件的m.
ⅰ)当m≥1时,函数g(t)的最大值为g(1)=m2+6m-4,
令m2+6m-4=3m,得m=1(m=-4舍去),
ⅱ)当m≤-1时,函数g(t)的最大值为g(-1)=m2+2m-4,
令m2+2m-4=3m,得m=
1-
| ||
| 2 |
1+
| ||
| 2 |
ⅲ)当-1<m<1时,函数g(t)的最大值为g(m)=2m2+4m-3,
令2m2+4m-3=3m,得m=-
| 3 |
| 2 |
综上,存在m使得f(x)的最大值为3m.m=1或m=
1-
| ||
| 2 |
点评:本题主要考查函数的最值的计算,利用换元法将函数转化为一元二次函数,利用二次函数的单调性是解决本题的关键.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDES,SA=AB=AE=2,BC=DE=
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDES,SA=AB=AE=2,BC=DE=
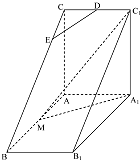 如图,直三棱柱ABC=A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点且
如图,直三棱柱ABC=A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点且