题目内容
已知数列{
}的前n项和Sn.
(1)计算S1、S2、S3、S4;
(2)猜想Sn的表达式,并用数学归纳法证明;
(3)对于任意的正整数n都有Sn<m,求实数m的取值范围.
| 1 |
| (3n-2)(3n+1) |
(1)计算S1、S2、S3、S4;
(2)猜想Sn的表达式,并用数学归纳法证明;
(3)对于任意的正整数n都有Sn<m,求实数m的取值范围.
考点:数学归纳法,数列的求和
专题:计算题,点列、递归数列与数学归纳法
分析:(1)利用条件,代入计算,可得S1、S2、S3、S4;
(2)猜想Sn的表达式,运用数学归纳法证明步骤进行证明;
(3)Sn=
=
(1-
),随着n增大,Sn增加,但Sn<
,即可求实数m的取值范围.
(2)猜想Sn的表达式,运用数学归纳法证明步骤进行证明;
(3)Sn=
| n |
| 3n+1 |
| 1 |
| 3 |
| 1 |
| 3n+1 |
| 1 |
| 3 |
解答:
解:(1)S1=
,S2=
,S3=
,S4=
;
(2)由(1)可以猜想Sn=
①当n=1时,显然成立;
②假设n=k,Sk=
,
当n=k+1时,Sk+1=Sk+ak+1=
+
=
=
,
说明n=k+1时,猜想也成立;
综合①②,猜想Sn=
成立.
(3)Sn=
=
(1-
),随着n增大,Sn增加,但Sn<
,由于Sn<m对任意的正整数n成立,
所以m≥
即可.
| 1 |
| 4 |
| 2 |
| 7 |
| 3 |
| 10 |
| 4 |
| 13 |
(2)由(1)可以猜想Sn=
| n |
| 3n+1 |
①当n=1时,显然成立;
②假设n=k,Sk=
| k |
| 3k+1 |
当n=k+1时,Sk+1=Sk+ak+1=
| k |
| 3k+1 |
| 1 |
| (3k+4)(3k+1) |
| (k+1)(3k+1) |
| (3k+4)(3k+1) |
| k+1 |
| 3k+4 |
说明n=k+1时,猜想也成立;
综合①②,猜想Sn=
| n |
| 3n+1 |
(3)Sn=
| n |
| 3n+1 |
| 1 |
| 3 |
| 1 |
| 3n+1 |
| 1 |
| 3 |
所以m≥
| 1 |
| 3 |
点评:本题考查数列的通项与求和,考查数学归纳法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
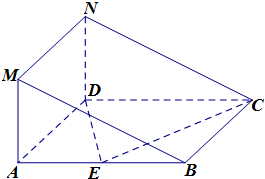 如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=
如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=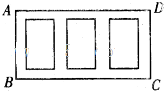 如图,某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的小矩形绿化区,这三块绿化区四周和绿化区之间分别设有2米宽和1米宽的走道,已知三块绿化区的总面积为600平方米,求该矩形区域ABCD占地面积的最小值.
如图,某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的小矩形绿化区,这三块绿化区四周和绿化区之间分别设有2米宽和1米宽的走道,已知三块绿化区的总面积为600平方米,求该矩形区域ABCD占地面积的最小值.