题目内容
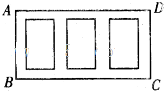如图，某广场要划定一矩形区域ABCD，并在该区域内开辟出三块形状大小相同的小矩形绿化区，这三块绿化区四周和绿化区之间分别设有2米宽和1米宽的走道，已知三块绿化区的总面积为600平方米，求该矩形区域ABCD占地面积的最小值．考点：基本不等式在最值问题中的应用
专题：应用题,函数的性质及应用
分析：由题意，设绿化区域小矩形的一边长为x，另一边长为y，则3xy=600，写出SABCD=（3x+6）（y+4）并化简，利用基本不等式求最值．
解答：
解：设绿化区域小矩形的一边长为x，另一边长为y，则
3xy=600，
∴SABCD=（3x+6）（y+4）=3xy+6（2x+y）+24
=624+6（2x+y）≥624+12
=624+12×20=864，
（当且仅当2x=y=20时，等号成立）
∴该矩形区域ABCD占地面积的最小值为864m2．
3xy=600，
∴SABCD=（3x+6）（y+4）=3xy+6（2x+y）+24
=624+6（2x+y）≥624+12
| 2yx |
=624+12×20=864，
（当且仅当2x=y=20时，等号成立）
∴该矩形区域ABCD占地面积的最小值为864m2．
点评：本题考查了学生将实际问题转化的为数学问题的能力，应用了基本不等式求最值，注意一正二定三相等．
练习册系列答案
相关题目
在△ABC中，a=2，A=45°，若此三角形有两解，则b的范围为（ ）
A、2＜b＜2
| ||||
| B、b＞2 | ||||
| C、b＜2 | ||||
D、
|