题目内容
已知函数f(x)=x2+ax+1(a>0).
(1)设g(x)=(2x+1)f(x),若y=g(x)与x轴恰有两个不同的交点,试求a的取值集合;
(2)设h(x)=f(x)-x2-|1-
|(x∈(0,2]),是否同时存在实数m和M(M>m),使得对每一个t∈(m,M),直线y=t与曲线y=h(x)恒有三个公共点?若存在,求出M-m的最大值I(a);若不存在,说明理由.
(1)设g(x)=(2x+1)f(x),若y=g(x)与x轴恰有两个不同的交点,试求a的取值集合;
(2)设h(x)=f(x)-x2-|1-
| 1 |
| x |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:(1)根据题意,函数y=g(x)与x轴恰有两个不同的交点,即方程g(x)=0有两个不相等的实数根,求出a的取值集合;
(2)根据x∈(0,2],去掉绝对值,求出h(x)的单调区间,画出函数图象,结合图象求出符合条件a的取值范围,从而求出M-m的最大值I(a).
(2)根据x∈(0,2],去掉绝对值,求出h(x)的单调区间,画出函数图象,结合图象求出符合条件a的取值范围,从而求出M-m的最大值I(a).
解答:
解:(1)∵函数f(x)=x2+ax+1(a>0),g(x)=(2x+1)f(x),
∴g(x)=(2x+1)(x2+ax+1),
当y=g(x)与x轴恰有两个不同的交点时,
方程x2+ax+1=0有两个相等的实数根,
∴△=a2-4=0,
解得a=2或a=-2(不合题意,舍去),
∴a的取值集合是{2};
(2)∵h(x)=f(x)-x2-|1-
|(x∈(0,2]),
∴当0<x≤1时,1≤
,
h(x)=(x2+ax+1)-x2-
+1=ax-
+2;
当1<x≤2时,1>
,
h(x)=(x2+ax+1)-x2-1+
=ax+
;
∴h(x)=
;
又∵0<x≤1时,h(x)=ax-
+2是单调增函数,h(x)≤a+1;
1<x≤2时,h(x)=ax+
,
h′(x)=a-
=
,
令h′(x)=0,得x=
,
∴当1≤
≤2,即
≤a≤1时,在x=
时,h(x)取得最小值2
,
且h(x)在(1,
)上是减函数,在(
,2]上是增函数,如图所示;
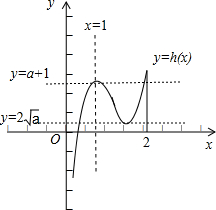 ;
;
若存在实数m和M(M>m),使得对每一个t∈(m,M),直线y=t与曲线y=h(x)恒有三个公共点,
则a+1>2
,∴(
-1)2>0,即a≠1,
∴
≤a<1①;
又h(2)≥h(1),即2a+
≥a+1,∴a≥
②;
由①②得,
≤a<1;
综上,M-m的最大值I(a)=(a+1)-2
=(
-1)2=(
-1)2=
-
.
∴g(x)=(2x+1)(x2+ax+1),
当y=g(x)与x轴恰有两个不同的交点时,
方程x2+ax+1=0有两个相等的实数根,
∴△=a2-4=0,
解得a=2或a=-2(不合题意,舍去),
∴a的取值集合是{2};
(2)∵h(x)=f(x)-x2-|1-
| 1 |
| x |
∴当0<x≤1时,1≤
| 1 |
| x |
h(x)=(x2+ax+1)-x2-
| 1 |
| x |
| 1 |
| x |
当1<x≤2时,1>
| 1 |
| x |
h(x)=(x2+ax+1)-x2-1+
| 1 |
| x |
| 1 |
| x |
∴h(x)=
|
又∵0<x≤1时,h(x)=ax-
| 1 |
| x |
1<x≤2时,h(x)=ax+
| 1 |
| x |
h′(x)=a-
| 1 |
| x2 |
| ax2-1 |
| x2 |
令h′(x)=0,得x=
| 1 | ||
|
∴当1≤
| 1 | ||
|
| 1 |
| 4 |
| 1 | ||
|
| a |
且h(x)在(1,
| 1 | ||
|
| 1 | ||
|
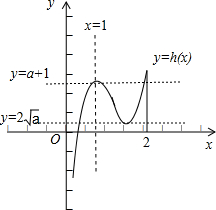 ;
;若存在实数m和M(M>m),使得对每一个t∈(m,M),直线y=t与曲线y=h(x)恒有三个公共点,
则a+1>2
| a |
| a |
∴
| 1 |
| 4 |
又h(2)≥h(1),即2a+
| 1 |
| 2 |
| 1 |
| 2 |
由①②得,
| 1 |
| 2 |
综上,M-m的最大值I(a)=(a+1)-2
| a |
| a |
|
| 3 |
| 2 |
| 2 |
点评:本题考查了函数的图象与性质的应用问题,也考查了分段函数的应用问题以及导数的应用问题,考查了数形结合的应用问题,是综合性题目.

练习册系列答案
相关题目
已知A={x|-1<x<1},B={x|x≤-1或x≥0},则A∩B=( )
| A、{x|-1<x<1} |
| B、{x|0<x<1} |
| C、{x|x≥0} |
| D、{x|0≤x<1} |
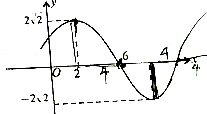 函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)的图象的一部分如图所示.
函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)的图象的一部分如图所示.