题目内容
已知数列{an}中,a1=1,二次函数f(x)=
an•x2+(2-n-an+1)•x的对称轴为x=
.
(1)试证明{2nan}是等差数列,并求{an}通项公式;
(2)设{an}的前n项和为Sn,试求使得Sn<3成立的n值,并说明理由.
| 1 |
| 2 |
| 1 |
| 2 |
(1)试证明{2nan}是等差数列,并求{an}通项公式;
(2)设{an}的前n项和为Sn,试求使得Sn<3成立的n值,并说明理由.
考点:等差数列的通项公式,二次函数的性质,等差数列的前n项和
专题:点列、递归数列与数学归纳法
分析:(1)根据对称轴,得到2n+1an+1-2nan=2,继而得到{2nan}是以2为首项,以2公差的等差数列,根据等差数列的通项公式求出an,
(2)利用错位相加法求出数列的前n项和为Sn,并利用函数的思想,得到Sn<3成立的n值.
(2)利用错位相加法求出数列的前n项和为Sn,并利用函数的思想,得到Sn<3成立的n值.
解答:
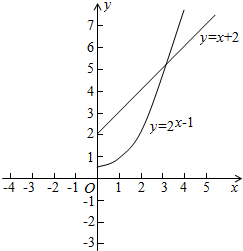 证明:(1)∵二次函数f(x)=
证明:(1)∵二次函数f(x)=
an•x2+(2-n-an+1)•x的对称轴为x=
.
∴
=
,
∴2n+1an+1-2nan=2,
∵a1=1,
∴2a1=2,
∴{2nan}是以2为首项,以2公差的等差数列,
∴2nan=2+2(n-1)=2n,
∴an=
=n•(
)n-1.
(2)∵Sn=a1+a2+…+an=1×
+2×
+3×
+…+n•(
)n-1,
∴
Sn=1×
+2×
+3×
+…+n•
,
两式相减得,
Sn=
+
+
+
+…+
-n•
=
-n•
=2-
•
-n•
,
∴Sn=4-
,
∵Sn<3,
∴4-
<3
∴n+2>2n-1,
分别画出函数y=x+2(x>0),与y=2x-1(x>0)的图象,如图所示
由图象可知,当n=1,2,3时,Sn<3成立.
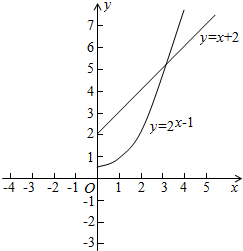 证明:(1)∵二次函数f(x)=
证明:(1)∵二次函数f(x)=| 1 |
| 2 |
| 1 |
| 2 |
∴
an+1-
| ||
| an |
| 1 |
| 2 |
∴2n+1an+1-2nan=2,
∵a1=1,
∴2a1=2,
∴{2nan}是以2为首项,以2公差的等差数列,
∴2nan=2+2(n-1)=2n,
∴an=
| 2n |
| 2n |
| 1 |
| 2 |
(2)∵Sn=a1+a2+…+an=1×
| 1 |
| 21-1 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
两式相减得,
| 1 |
| 2 |
| 1 |
| 20 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
1-
| ||
1-
|
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 2n |
∴Sn=4-
| n+2 |
| 2n-1 |
∵Sn<3,
∴4-
| n+2 |
| 2n-1 |
∴n+2>2n-1,
分别画出函数y=x+2(x>0),与y=2x-1(x>0)的图象,如图所示
由图象可知,当n=1,2,3时,Sn<3成立.
点评:本题考查二次函数的性质,以及等差关系的确定,错位相减法求数列的和,培养可学生的转化思想与综合运算、推理证明能力,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
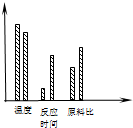 如图,是某正交试验设计中绘制的产量和因素的关系图,由此图可知( )
如图,是某正交试验设计中绘制的产量和因素的关系图,由此图可知( )| A、影响试验结果最主要的因素是温度 |
| B、影响试验结果最主要的因素是反应时间 |
| C、影响试验结果最主要的因素是原料比 |
| D、因图中数据不全,无法分清哪个因素影响最大 |
已知曲线C:
-y2=1的左右焦点分别为F1F2,过点F2的直线与双曲线C的右支相交于P,Q两点,且点P的横坐标为2,则PF1Q的周长为( )
| x2 |
| 3 |
A、
| ||||
B、5
| ||||
C、
| ||||
D、4
|
由曲线y=x2,y=
围成的封闭图形的面积为( )
| x |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
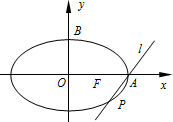 在平面直角坐标系xOy中,椭圆
在平面直角坐标系xOy中,椭圆