题目内容

由二项式定理知识可将[（x+y）n-（x-y）n]（n∈N*）展开并化简．若a=
∫
26
0
(
1
2
x
)dx，则在（a+5）2n+1（n∈N*）的小数表示中，小数点后面至少连续有零的个数是（　　）
A、2n-1B、2n
C、2n+1D、2n+2
考点：二项式定理的应用,定积分
专题：综合题,二项式定理
分析：先求出a，利用(
26
+5)2n+1与(
26
-5)2n+1的小数部分完全相同，即可得出结论．
解答： 解：因为a=
∫
26
0
(
1
2
x
)dx=
x
|
26
0
=
26

由题目给出的提示：由二项式定理[(
26
+5)2n+1-(
26
-5)2n+1]∈Z，
因此(
26
+5)2n+1与(
26
-5)2n+1的小数部分完全相同．
∵0＜
26
-5＜
1
26
+5
＜
1
10
，
∴0＜(
26
-5)2n+1＜(
1
26
+5
)2n+1＜(
1
10
)2n+1，
即(
26
-5)2n+1的小数表示中小数点后面至少接连有2n+1个零，
因此，(
26
+5)2n+1的小数表示中，小数点后至少连续有2n+1个零．
故选C．
点评：本题考查简单定积分的计算和二项式定理的应用以及化归的数学思想．
练习册系列答案
相关题目
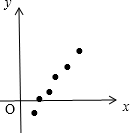
已知变量x，y之间具有相关关系，其散点图如图所示，则其回归直线方程可能是（　　）
A、y=2x-1
B、y=2x+1
C、y=-2x+1
D、y=-2x-1
已知角α的顶点在坐标原点，始边与x轴的正半轴重合，角α的终边与圆心在原点的单位圆（半径为1的圆）交于第二象限内的点A(xA，
4
5
)，则sin2α=
 
．（用数值表示）
已知定义在R上的函数f（x）=-f（x+
3
2
），且f（-2）=f（-1）=-1，f（0）=2，f（1）+f（2）+…+f（2009）+f（2010）=
 
．
已知函数f（x）=x2+ax+1（a＞0）．
（1）设g（x）=（2x+1）f（x），若y=g（x）与x轴恰有两个不同的交点，试求a的取值集合；
（2）设h（x）=f（x）-x2-|1-
1
x
|（x∈（0，2]），是否同时存在实数m和M（M＞m），使得对每一个t∈（m，M），直线y=t与曲线y=h（x）恒有三个公共点？若存在，求出M-m的最大值I（a）；若不存在，说明理由．
（
x
-
2
3x
）5的展开式中的常数项是
 
（用数字作答）．
实数x，y满足不等式
y≥1
x+y≥3
x-2y-2≤0
，则ω=
y+1
x+1
的取值范围是（　　）
A、[-1，
2
5
]
B、[-1，
2
3
]
C、（-∞，-1]∪[
2
5
，+∞）
D、（-∞，-1）∪（
2
5
，+∞）
已知f（x）=
1
1+4
1
2
-x
．
（1）求f（x）+f（1-x）的值；
（2）求f（
1
1001
）+f（
2
1001
）+f（
3
1001
）+…+f（
1000
1001
）的值．
（1）四个不同的小球放入四个不同的盒中，一共有
 
种不同的放法．
（2）四个相同的小球放入四个不同的盒中，一共有
 
种不同的放法．
（3）四个不同的小球放入四个不同的盒中且恰好有一个空盒的放法有
 
种．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网