题目内容
已知f(x)=x2+2(a-1)+3的单调递减区间是(-∞,3],则实数a为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:函数f(x)=x2+2(a-1)x+3在区间(-∞,3]上是减函数,即说明(-∞,3]是函数f(x)的减区间的子集.
解答:
解:函数f(x)=x2+2(a-1)x+3的单调减区间为(-∞,1-a],
又f(x)在区间(-∞,3]上是减函数,
所以有(-∞,3]⊆(-∞,1-a],
所以3≤1-a,解得a≤-2,即实数a的取值范围为(-∞,-2].
故答案为:(-∞,-2].
又f(x)在区间(-∞,3]上是减函数,
所以有(-∞,3]⊆(-∞,1-a],
所以3≤1-a,解得a≤-2,即实数a的取值范围为(-∞,-2].
故答案为:(-∞,-2].
点评:本题考查函数单调性的性质,函数f(x)在某区间上单调,意味着该区间为函数单调区间的子集,而未必是单调区间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设
(x+1)k=a0+a1x+a2x2+a3x3+…+a100x
,则
=( )
| 100 |
 |
| k=1 |
| 100 |
| a4 |
| a5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
实数x,y满足不等式
,则ω=
的取值范围是( )
|
| y+1 |
| x+1 |
A、[-1,
| ||
B、[-1,
| ||
C、(-∞,-1]∪[
| ||
D、(-∞,-1)∪(
|
点P(x,y)在不等式组
表示的平面区域内,若点P(x,y)到直线y=kx-1的最大距离为2
,则k为( )
|
| 2 |
| A、-1 | B、-1或1 |
| C、-1或2 | D、1 |
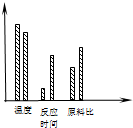 如图,是某正交试验设计中绘制的产量和因素的关系图,由此图可知( )
如图,是某正交试验设计中绘制的产量和因素的关系图,由此图可知( )| A、影响试验结果最主要的因素是温度 |
| B、影响试验结果最主要的因素是反应时间 |
| C、影响试验结果最主要的因素是原料比 |
| D、因图中数据不全,无法分清哪个因素影响最大 |
已知曲线C:
-y2=1的左右焦点分别为F1F2,过点F2的直线与双曲线C的右支相交于P,Q两点,且点P的横坐标为2,则PF1Q的周长为( )
| x2 |
| 3 |
A、
| ||||
B、5
| ||||
C、
| ||||
D、4
|