题目内容
18.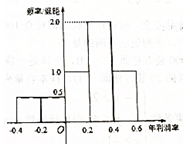 某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.
某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.(1)利用调研数据估计明年远洋捕捞队的利润ξ的分布列和数学期望Eξ.
(2)为确保本地的鲜鱼供应,市政府要求该公司对本地养鱼场的投资不得低于远洋捕捞队的一半.适用调研数据,给出公司分配投资金额的建议,使得明年两个项目的利润之和最大.
分析 (1)随机变量ξ的可能取值为0.6y,0,-0.3y,分别求出相应的概率,由此能求出随机变量ξ的分布列和Eξ.
(2)根据题意得,x,y满足的条件,由频率分布直方图求出本地养鱼场的年平均利润率为0.20x千万元,从而明年连个个项目的利润之和为z=0.2x+0.3y,作出x,y满足的可行域,由此能求出公司投资本地养鱼场和远洋捕捞队的资金应分别为2千万元、4千万元时,明年两个项目的利润之和的最大值为1.6千万元.
解答 解:(1)随机变量ξ的可能取值为0.6y,0,-0.3y,
随机变量ξ的分布列为,
| ξ | 0.6y | 0 | -0.3y |
| P | 0.6 | 0.2 | 0.2 |
(2)根据题意得,x,y满足的条件为$\left\{{\begin{array}{l}{x+y≤6}\\{x≥\frac{1}{2}y}\\{x≥0}\\{y≥0}\end{array}}\right.$①,

由频率分布直方图得本地养鱼场的年平均利润率为:
-0.3×0.2×0.5+(-0.1)×0.2×0.5+0.1×0.2×1.0+0.3×0.2×2.0+0.5×0.2×1.0=0.20,
∴本地养鱼场的年利润为0.20x千万元,
∴明年连个个项目的利润之和为z=0.2x+0.3y,
作出不等式组①所表示的平面区域若下图所示,即可行域.
当直线z=0.2x+0.3y经过可行域上的点M时,截距$\frac{z}{0.3}$最大,即z最大.
解方程组$\left\{{\begin{array}{l}{x+y=6}\\{x=\frac{1}{2}y}\end{array}}\right.$,得$\left\{{\begin{array}{l}{x=2}\\{y=4}\end{array}}\right.$
∴z的最大值为:0.20×2+0.30×4=1.6千万元.
即公司投资本地养鱼场和远洋捕捞队的资金应分别为2千万元、4千万元时,明年两个项目的利润之和的最大值为1.6千万元.
点评 本题考查频率分布直方图、离散型随机变量的分布列、数学期望、线性规划等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查数形结合思想,是中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
9.“(x-1)(x+2)=0”是“x=1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.已知函数f(x)=sin(ωx+$\frac{π}{3}$)-$\frac{1}{2}$cos(ωx-$\frac{7π}{6}$)(ω>0),满足f(-$\frac{π}{6}$)=$\frac{3}{4}$,则满足题意的ω的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
3.若点P是曲线$y=\frac{3}{2}{x^2}-2lnx$上任意一点,则点P到直线$y=x-\frac{5}{2}$的距离的最小值为( )
| A. | $\sqrt{2}$ | B. | $\frac{{3\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{5}$ |
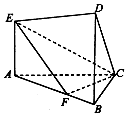 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB