题目内容
3．若点P是曲线$y=\frac{3}{2}{x^2}-2lnx$上任意一点，则点P到直线$y=x-\frac{5}{2}$的距离的最小值为（ ）| A． | $\sqrt{2}$ | B． | $\frac{{3\sqrt{3}}}{2}$ | C． | $\frac{{3\sqrt{2}}}{2}$ | D． | $\sqrt{5}$ |
分析 由题意作图，故当点P是曲线的切线中与直线$y=x-\frac{5}{2}$平行的直线的切点时，距离最小；从而解得．
解答 解：由题意作图如下，
当点P是曲线的切线中与直线y=x-2平行的直线的切点时，距离最小；
曲线$y=\frac{3}{2}{x^2}-2lnx$
故令y′=3x-$\frac{2}{x}$=1解得，x=1；
故点P的坐标为（1，$\frac{3}{2}$）；
故点P到直线y=x-$\frac{5}{2}$的最小值为：$\frac{|1-\frac{3}{2}-\frac{5}{2}|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$；
故选：C．
点评 本题考查了几何意义的运用及导数的综合应用，属于中档题．
练习册系列答案
相关题目
13．平面α过正方体ABCD-A1B1C1D1的面对角线$AB_1^{\;}$，且平面α⊥平面C1BD，平面α∩平面ADD1A1=AS，则∠A1AS的正切值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{1}{2}$ |
11．函数f（x）的定义域是（0，$\frac{π}{2}$），f′（x）是它的导函数，且f（x）+tanx•f′（x）＞0在定义域内恒成立，则（ ）
| A． | f（$\frac{π}{6}$）＞$\sqrt{2}$f（$\frac{π}{4}$） | B． | $\sqrt{2}$sin1•f（1）＞f（$\frac{π}{4}$） | C． | f（$\frac{π}{6}$）＞$\sqrt{3}$f（$\frac{π}{3}$） | D． | $\sqrt{2}$f（$\frac{π}{4}$）＞$\sqrt{3}$f（$\frac{π}{3}$） |
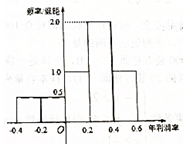某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队．经过本地养鱼场年利润率的调研，得到如图所示年利润率的频率分布直方图．对远洋捕捞队的调研结果是：年利润率为60%的可能性为0.6，不赔不赚的可能性为0.2，亏损30%的可能性为0.2．假设该公司投资本地养鱼场的资金为x（x≥0）千万元，投资远洋捕捞队的资金为y（y≥0）千万元．
8．一个学校高一、高二、高三的学生人数之比为2：3：5，若用分层抽样的方法抽取容量为200的样本，则应从高三学生中抽取的人数为（ ）
| A． | 40 | B． | 60 | C． | 80 | D． | 100 |
15．
为了解甲、乙两厂产品的质量，从甲厂生产的产品中随机抽取3件样品，从乙厂生产的产品中随机抽取4件样品，测量产品中某种元素的含量（单位：毫克），如图是测量数据的茎叶图．若它们的中位数相同，平均数也相同，则图中的m，n的比值$\frac{m}{n}$=（ ）
为了解甲、乙两厂产品的质量，从甲厂生产的产品中随机抽取3件样品，从乙厂生产的产品中随机抽取4件样品，测量产品中某种元素的含量（单位：毫克），如图是测量数据的茎叶图．若它们的中位数相同，平均数也相同，则图中的m，n的比值$\frac{m}{n}$=（ ）| A． | 1 | B． | $\frac{1}{3}$ | C． | $\frac{8}{3}$ | D． | $\frac{3}{8}$ |
如图，在四棱锥P-ABCD中，PA⊥面ABCD，AB∥CD，CD⊥AD，AD=CD=2AB=2，E，F分别为PC，CD的中点